Póta György
KLTE Fizikai Kémiai Tanszéke, Debrecen, Pf.7, 4010
1. Bevezetés
4. Az autokatalitikus hullám sebessége
6. Kolmogorov, Petrovszkij és Piszkunov tétele
8. Hullámok a nitrát-ferroin reakcióban és más salétromsavas oxidációkban
9. Hullámok és térbeli szerkezetek a Belouszov-Zsabotyinszkij-reakcióban
10. Stacionárius térbeli szerkezetek (Turing-struktúrák)
12. Irodalom
12a. Kapcsolódó témák a hálózaton
A kémiai hullámok bizonyos fajtái mindennapi életünk eléggé gyakori szereplői. A meggyújtott gyufaszálon vagy cigarettán végighaladó láng, a gyújtózsinór égése vagy a bozóttűz kémiai hullámnak tekinthető, mivel a kémiai reakció végigvonul a térbelileg kiterjedt rendszeren. Az első pillanatban bizonyára meglepő, ha azt állítjuk, hogy közönséges hőmérsékleten, oldatokban olyan terjedő reakciófrontok létezhetnek, amelyek mozgása például a gyújtózsinóron terjedő láng tökéletes analogonja. Ezek az oldatbeli hullámok azonban kevésbé mindennaposak, velük legtöbbször csak a laboratóriumban találkozhatunk. Ugyanakkor az oldatbeli kémiai hullámoknak magukon túlnövő jelentőséget ad, hogy ilyen típusú hullámok feltehetően szerepet kapnak az élő szervezetek különféle információtovábbító, növekedési és alakváltoztatási folyamataiban (Nicolis és Prigogine, 1978).
Bár az oldatbeli hullámok kísérleti és elméleti vizsgálata Luther (1906) úttörő munkájáig nyúlik vissza, a terület részletes vizsgálata csupán az 1960-as években - a Belouszov-Zsabotyinszkij-reakció (BZ-reakció) felfedezése (Belouszov, 1959) után - kezdődött meg. A hullámjelenségeket bizonyítottan mutató kémiai rendszerekről az 1.1. táblázat ad felvilágosítást.
| rendszer | hivatkozás |
| permanganát + oxalát | Luther, 1906 |
| alkilszulfát hidrolízis | Luther, 1906 |
| salétromsav + jodid | Luther, 1906 |
| bromát + arzenit | Luther, 1906 |
| jodát + arzenit | Epik és Shub, 1955; Gribschaw és mtsai, 1981; Hanna és mtsai, 1982; Harrison és Showalter, 1986 |
| jodát-Ce(IV)-Mn(II)-szerves szubsztrátumok | Rastogi és mtsai, 1985 |
| bromát + ferroin | Showalter, 1981 |
| klorit + jodid | Weitz és Epstein, 1984 |
| klorit + jodid + malonsav | De Kepper és mtsai, 1982 |
| klorit + jodid +malonsav (Turing) | Castets és, mtsai, 1990 |
| klorit + tioszulfát | Nagypál és mtsai, 1986 |
| salétromsav + dimetil-szulfid | Rudakov és mtsai, 1973 |
| salétromsav + hidroxil-amin | Gowland és Stedman, 1983 |
| salétromsav + hidroxil-amin + nátrium-tiocianát | Gowland és mtsai, 1986 |
| salétromsav + vas(II) | Bazsa és Epstein, 1985; Nagypál és mtsai, 1986; Póta és mtsai, 1991 |
| salétromsav + ferroin | Póta és mtsai, 1989 |
| hidrogén-peroxid + jód | Furrow, 1987 |
| oxianionok savkatalizált oxidációja | Szirovicza és mtsai, 1989 |
| benzaldehid autooxidációja | Boga és mtsai, 1990 |
| Belouszov-Zsabotyinszkij-reakció | Vidal és Hanusse, 1986 (összefoglaló) |
| jodát + szulfit + ferrocianid | Lee és mtsai, 1993 |
Kémiai hullámok és térbeli szerkezetek (Bazsa, 1987/88 nyomán)
Az oldatbeli kémiai hullámok ismertetését a viszonylag egyszerű autokatalitikus hullámokkal kezdjük.
Célszerű először az autokatalízis fogalmát bemutatnunk. Tekintsük az
(2.0a) U + V --> 2V
(2.0b) r = kuv
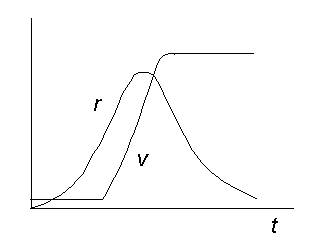
kémiai reakciót, ahol r a reakciósebesség koncentrációfüggését leíró sebességi egyenlet. A (2.0) reakcióban a V anyagból több keletkezik, mint amennyi elfogy, s (2.0b) mutatja, hogy U állandó koncentrációja mellett r növekszik, ha V koncentrációja nő. Ilyen módon V elősegíti saját képződését (autokatalízis). Az U anyagfajta neve szubsztrátum, V pedig az ún. autokatalizátor. Anyag beáramlásától mentes - zárt - rendszerben a reakciósebesség időben először nő, majd amikor U fogyása hangsúlyossá válik, maximumon áthaladva csökkenni kezd. A V autokatalizátor koncentrációja ennek megfelelően időben S-alakú görbe szerint változik (2.1. ábra).

r: sebesség - idő; v: koncentráció - idő görbe homogén rendszerben lejátszódó autokatalitikus reakcióban.
A jól kevert, zárt edényben lezajló (2.0) reakcióban a reaktánsok koncentrációjának (u és v) időbeli változását a reakciókinetikai törvényekből következő
(2.1) dv/dt = kuv; du/dt = -kuv
közönséges differenciálegyenlet-rendszer írja le. A rendszerre érvényes az anyag megmaradását kifejező
(2.2) u(t) + v(t) = u0+v0
első integrál, ahol a 0 index a kezdeti koncentrációt jelöli. Mivel a reakcióban U teljesen elfogy, V végső koncentrációja (vinf) (2.2) jobb oldalával egyezik meg. A szokásos esetekben v0 << u0 teljesül, ezért jó közelítéssel vinf = u0.
Az autokatalitikus reakciók sebességi egyenlete általánosságban eléggé sokféle lehet, ezért (2.0) helyett az
(2.3a) nU + mV --> pV; p > m
(2.3b) r = g(u)va
egyenleteket írhatjuk. Itt a nem rögzített g függvény a szubsztrátum hatásának sokféleségére utal, a pedig - amely rendszerint egész szám - az autokatalízis rendjét adja meg. (A g függvény matematikai szempontból eleget tesz bizonyos természetes feltevéseknek, például nemnegatív u értékekre van értelmezve, itt folytonosan differenciálható, g(u) > 0, ha u > 0 és g(0) = 0.) Mindaz, amit az előzőekben vázoltunk, a (2.3) szerinti autokatalízisre is érvényes. Az autokatalízis és egyéb kinetikai jelenségek részletes formálkinetikai tárgyalását illetően Schubert (1976) munkájára utalunk.
3. A terjedő reakciófront
Valósítsuk meg a (2.0) reakciót úgy, hogy az U szubsztrátumot u0 koncentrációjú homogén oldatban tartalmazó hosszú cső végébe autokatalizátort (V) juttatunk. Az autokatalizátort tartalmazó térfogatelemben az autokatalitikus reakció gyorsan lejátszódik, V mennyisége felszaporodik, U mennyisége zérusra csökken. Mivel a szomszédos térfogatelemben még nincs V, óriási koncentrációgradiens alakul ki, amelynek következtében V gyorsan a szomszédos térfogatelembe diffundál, és ott is beindítja az autokatalitikus reakciót. Az autokatalizátor tehát újabb térfogatelemekbe vándorolhat, és ilyen módon a reakció végighalad a cső mentén. A térbeli és időbeli koncentrációviszonyokat minőségileg a 3.1. ábra mutatja be.
![[acwav.gif]](acwav.gif)
Egyszerű autokatalitikus hullám terjedési mechanizmusa és koncentráció-eloszlása; sötét cella: nagy autokatalizátor-koncentráció; szürke cella: kis autokatalizátor-koncentráció; fehér cella: zérus autokatalizátor-koncentráció
A reakciófront bizonyos előrehaladtával a front mögötti tartományban felhalmozódik a V autokatalizátor, a front előtt pedig továbbra is az érintetlen U szubsztrátumot tartalmazó elegy van.
A kialakuló reakciófront mozgását - tehát a hullámot - úgy írhatjuk le, hogy az U és V diffúziójára vonatkozó Fick-féle differenciálegyenletekbe a kémiai reakció - mint anyagforrás és nyelő - hozamát is belefoglaljuk:
(3.1a) u't = Duu''xx - kuv
(3.1b) v't = Dvv''xx + kuv,
ahol t az idő, x a térkoordináta, Du és Dv pedig a megfelelő diffúziós együtthatók. Ezeket az egyenleteket számítógépes módszerrel mindig megoldhatjuk (lásd 7. pont), szemléletesebb eredményt kapunk azonban, ha analitikus megfontolásokkal próbálkozunk.
4. Az autokatalitikus hullám sebessége
Az autokatalitikus hullám sebességére vonatkozó legegyszerűbb - heurisztikus - gondolatmenet a következő (Showalter és Tyson, 1987): Tételezük fel, hogy az U szubsztrátum koncentrációját a hullámra vonatkozó kísérlet alatt anyagbeáramlással az állandó u0 értéken tartjuk. Ez a valóságban nehezen valósítható meg, matematikailag azonban megkönnyíti a dolgunkat, hiszen így a vizsgálandó differenciálegyenlet lineáris lesz:
(4.1) v't = Dvv''xx + ku0v.
Tekintsük egyenletünknek azt a megoldását, amely kezdetben a v0 erősségű pontszerű forrásnak felel meg:
(4.2) v(x, t) = v0 exp(ku0t - x2/4Dvt) (4 pi Dvt)-1/2.
A (4.2) képlet növekvő t értékekre nem korlátos, ez azonban csupán az állandó szubsztrátum-koncentráció következménye, és a lényegi mondanivalót nem zavarja. A reakciófrontot azon a helyen észleljük, ahol V koncentrációja elér egy kritikus vk értéket. A vk koncentrációhoz tartozó xk koordináta értéke az idővel változik, az xk pont - azaz a front - meghatározott módon mozog az x-tengely mentén. A mozgást jellemző függvényt a
(4.3) v(xk(t), t) = vk
egyenletből határozhatjuk meg. Elemi számolással belátható, hogy a dxk/dt hullámsebesség nagy t értékekre a
(4.4) c* = (4Dvku0)1/2
állandó értékhez tart. Ugyanezt a gondolatmenetet alkalmazhatjuk az általános (2.3) reakciónál is, feltéve, hogy a = 1. Ilyenkor a
(4.5) c* = (4Dvg(u0))1/2(m - n)1/2
terjedési sebességhez jutunk. Ha meggondoljuk, hogy az autokatalitikus hullám sebességét elsősorban a frontban uralkodó viszonyok szabják meg, akkor a (4.4) és (4.5) képleteknek jelentős igazságtartalmat kell tulajdonítanunk abban az esetben is, ha a kísérletben az U anyagfajta elfogy. Az autokatalitikus hullám ugyanis mindig olyan közegbe lép be, amely érintetlen szubsztrátumot tartalmaz, a frontban tehát jó közelítéssel u = u0. Érdemes megjegyezni, hogy a (4.4) képlethez lényegében már Luther (1906) is eljutott, de gondolatmenetét - úgy tudjuk - sehol sem közölte, így az máig ismeretlen. (Élvezetesen adja vissza a százed eleji konferencia hangulatát a konferencia-kiadványból készült cikk (angol fordítás: Luther, 1987), amelyben Luther beszámolóján kívül a kérdések (például Nernsté) és válaszok is benne vannak.)
Ha a hullámterjedésre vonatkozó kísérletet zárt rendszerként tárgyaljuk, az eddigiekhez képest mélyebb információkhoz juthatunk. Tételezzük fel, hogy a hullám leírását a valóságos kísérlet megindítása után elegendően sok idő elteltével kezdjük meg. Ekkor a tartóedényül szolgáló cső egy hosszú szakaszán már csak autokatalizátor, a másik szakaszán pedig továbbra is tiszta szubsztrátum lesz. Így a (3.1) egyenletekhez - nagyon éles elválasztó frontot feltételezve - a következő kezdeti feltételeket adhatjuk meg:
(5.1a) u(x, 0) = 0 ha x > 0 és u(x, 0) = u0 ha x < 0
(5.1b) v(x, 0) = u0 ha x > 0 és v(x, 0) = 0 ha x < 0.
Tételezzük fel, hogy U és V diffúziós együtthatója azonos, tehát Du = Dv = : D. Ekkor a
(5.2) h = u + v
függvény (3.1) és (5.1) alapján megoldása a teljes számegyenesen értelmezett, egyszerű
(5.3a) h't = Dh''xx
(5.3b) h(x, 0) = u0
diffúziós feladatnak, és ezért
(5.4) h = u0
teljesül minden x és t > 0 értékre. Az (5.4) egyenlet segítségével az autokatalizátor terjedését leíró egyváltozós
(5.5) v't = Dvv''xx + k(u0 - v)v,
feladathoz jutunk. Az (5.5) egyenlethez az (5.1b) kezdeti feltétel tartozik. Az általánosabb (2.3) reakcióval ismét végigcsinálhatjuk a fenti megfontolásokat, és eredményül az (5.5) egyenletet kapjuk a forrástagban fellépő értelemszerű különbséggel. Az (5.5) egyenlettel kapcsolatban Fisher (1937) jelentős eredményeket ért el.
Az egyetlen változóra redukált rendszerek leírásához ma már klasszikusnak számító matematikai elmélet áll rendelkezésünkre (Kolmogorov, Petrovszkij és Piszkunov, 1937). Ebben az elméletben (amelyet a továbbiakban KPP-elméletnek nevezünk) a
(6.1) v't = Dv''xx + f(v)
egyenletet vizsgáljuk, ahol D > 0, az elegendően sokszor differenciálható f függvényre pedig teljesülnek az
(6.2a) f(0) = f(1) = 0; f(v) > 0 ha 0 < v < 1
(6.2b) f'(0) > 0; f'(v) < f'(0) ha 0 < v =< 1
feltételek. A kezdeti feltétel a következő: b >= a esetén
(6.3) v(x, 0) = 1 ha x > b és v(x, 0) = 0 ha x < a.
A (6.1)-(6.3) meghatározta feladatnak az ún. hullámmegoldásait keressük, vagyis azokat, amelyek a
(6.4) v(x, t) = q(x + ct)
alakban írhatók fel, ahol c állandó. Könnyű belátni, hogy q rögzített t esetén olyan görbét ír le x függvényében, amely azután növekvő t értékekre változatlan alakban tolódik el az x-tengely mentén. Az eltolódás sebessége c. Ha a (6.4) összefüggést a (6.1) egyenletbe beírjuk, akkor a következőt kapjuk:
(6.5) Dq''(z) - cq'(z) + f(q(z)) = 0,
ahol z = x + ct. Legyen
(6.6) c* = (4Df'(0))1/2.
Kolmogorov, Petrovszkij és Piszkunov igazolták, hogy a (6.5) egyenletnek minden c >= c* értékre van olyan megoldása, amelyre 0 < v < 1 és ezenfelül
(6.7) v --> 1, ha z --> (végtelen) és v --> 0, ha z --> -(végtelen).
Igaz továbbá, hogy a (6.1)-(6.3) feladat megoldása (ami nem hullámmegoldás) tart a c* értékhez tartozó q* hullámmegoldáshoz a következő értelemben: létezik olyan m függvény, hogy
(6.8) |v(x, t) - q(x + c*t + m(t)| --> 0, ha t --> végtelen
egyenletesen x-ben; ezenfelül m'(t) --> 0, ha t --> végtelen.
Az (5.1) kezdeti feltételeknél a kísérletileg észlelt hullámsebességet tehát összevethetjük a c* sebességgel.
A c* sebességű hullám terjedése diffúzió nélkül lehetetlen volna, mivel ez a hullám olyan kezdeti feltételből indul, ahol V nincs jelen a jövőbeli terjedésnek megfelelő térrészben. Az ilyen típusú hullámokat tradicionálisan trigger hullámoknak nevezzük, a név persze inkább létrehozásukra, semmint terjedési módjukra utal. A c*-nál nagyobb c sebességű hullámmegoldások olyan kezdeti feltételekkel lehetnek kapcsolatban, ahol a V autokatalizátor jelen van a teljes reakciótérben, tehát a reakció egyidejűleg megindul minden térbeli pontban. Az ilyen pszeudohullámok vagy fázishullámok esetében tulajdonképpen a reakció térbeli fáziskülönbségét észleljük hullámként, a jelenségben a diffúzió nem játszik döntő szerepet. A pszeudohullámoknak elvben végtelen nagy sebességük is lehet. Ha ugyanis V kezdeti térbeli eloszlása igen lapos, azaz csaknem ugyanannyi V van jelen mindenütt, akkor állandó u0 szubsztrátum-koncentráció esetében a reakció adott fázisa csaknem ugyanakkor következik be egymástól távol levő helyeken is, azaz a hullám rövid idő alatt nagy távolságokat tesz meg.
Ha a (2.3b) reakciósebességi egyenletben a = 1, g(u) > 0, ha u > 0 és nincs inhibíció, azaz
(6.9) dg/du > 0,
akkor egyszerű számolással megmutatható, hogy a rendszerben mindig fellépnek KPP-hullámok. A c* sebességet explicit formában a (4.5) képlet adja meg.
A hullám térbeli koncentrációeloszlására, azaz profiljára vonatkozó (6.5) egyenletet a tipikusnak mondható nemlineáris esetekben általában nem tudjuk analitikusan megoldani. Vannak azonban olyan speciális körülmények, ahol megadható analitikus megoldás (lásd például Kaliappan, 1984).
A KPP-tétel nem mindig alkalmazható. Ez a helyzet például a kvadratikus autokatalízist leíró
(6.10a) U + 2V --> 3V; r = kuv2
reakció esetében. Gray és mtsai (1987) szerint ebben a rendszerben a releváns hullámmegoldás sebessége
(6.11) c = (Dku02/2)1/2.
Az
(6.12a) U + V --> 2V; r = k1uv
(6.12b) V --> C; r = k2v
rendszerben az autokatalitikus reakció az autokatalizátort fogyasztó folyamattal együtt lép fel. Merkin és mtsai (1989) szerint itt az autokatalitikus hullám sebessége
(6.13) c = [4D(k1u0 - k2)]1/2,
feltéve, hogy a kerek zárójeles mennyiség pozitív.
A hullámmegoldás létezésére vonatkozóan számos matematikai eredmény található Fife (1979) és Murray (1977, 1993) könyveiben.
Megfelelő számítógépes kapacitás esetén a reakció-diffúzió differenciálegyenleteket numerikusan is megoldhatjuk. Ez elsősorban bonyolult rendszereknél indokolt, ahol több, egymás mellett futó reakcióval kell számolnunk, és az eddig tárgyalt analitikus eljárások nem alkalmazhatók. A numerikus megoldás legtöbbször az angolszász nyelvterületen "method of lines" néven hivatkozott (Reusser és Field, 1979) eljárással történik. Ennek lényege a következő. Osszuk fel az x-tengelyt kicsiny h hosszúságú intervallumokra (cellákra), és vizsgáljuk ezekben a reakció és a diffúzió okozta koncentrációváltozásokat. Ha vi-1, vi és vi+1 rendre az (i - 1)-edik, i-edik és (i + 1)-edik intervallumban érvényes koncentráció, akkor a második térbeli deriváltat differenciahányadossal közelítve az i-edik intervallumbeli koncentrációra érvényes reakció-diffúzió differenciálegyenlet
(7.1) dvi/dt = D(vi+1 - 2vi + vi-1)/h2 + f
alakú, ahol f a kémiai reakciót jellemző forrástag-függvény. Érdemes hangsúlyozni, hogy itt már közönséges differenciálegyenletről van szó, nem pedig parciálisról. Ha az x-tengelyt N részre osztottuk, és a V komponensen kívül mások is vannak - összesen K komponens -, akkor NK számú, (7.1) alakú egyenletet kell megoldanunk. A gyakorlatilag fontos esetekben például N = 1000, K = 4, úgyhogy 4000 közönséges differenciálegyenletből álló rendszerrel állunk szemben. A reakció-diffúzió egyenletekből kapott közönséges differenciálegyenlet-rendszerek legtöbbször ún. "merev" (angolul "stiff") típusúak, hatékony megoldásukhoz speciális módszerek szükségesek (Gear, 1971; Kaps és Rentrop, 1979). A "method of lines" alkalmazása bizonyos óvatosságot igényel, mivel az eredmények erősen függhetnek a térbeli felosztás finomságától, azaz h nagyságától. Addig érdemes finomítani a felosztást, amíg a számítási eredmények már nem változnak lényegesen.
Megtehetjük azt is, hogy a vizsgálandó parciális differenciálegyenlet-rendszert hullámmegoldás feltételezésével közönséges differenciálegyenletekből álló rendszerre vezetjük vissza úgy, ahogyan azt egy egyenletnél a KPP-tétel alkalmazásakor láttuk. Ha a diffúziós együtthatókat és a terjedési sebességet valahonnan ismerjük, az egyetlen meghatározandó dolog a hullámmegoldás alakja, amely a peremérték-feladat megoldása. A konkrét számításokhoz többek között az ún. "shooting method" alkalmazható (Kubicek és Marek, 1983). Lényege, hogy a peremérték-feladatot - az első derivált kezdeti értékének alkalmas megválasztásával - egyenértékű kezdetiérték-feladatra vezeti vissza.
Az autokatalitikus hullámokkal kapcsolatos első modern vizsgálatokat Hanna és mtsai (1982) végezték a jodát-arzenit rendszerben. A példákat mégis a salétromsavas oxidációs reakciók családjából válogattuk, mert itt az egyes rendszerek közötti összefüggésekre is rámutathatunk.
A nitrát-ferroin reakcióban a ferroin (Fe(phen)32+) a
(8.0) 2Fe(phen)32+ + NO3- + 3H+ = 2Fe(phen)33+ + HNO2 + H2O
bruttó egyenlet szerint ferriinné (Fe(phen)33+) oxidálódik, a folyamat autokatalitikus, az autokatalizátor a salétromossav (HNO2). Az elméleti részben vázolt elrendezésben a piros/kék (ferroin/ferrin) hullámfront mozgása szabad szemmel is jól követhető. A (8.0) reakció a következő két részfolyamatra bontható (Lengyel és mtsai, 1988):
(8.1a) NO3- + HNO2 + H+ = 2NO2 + H2O
(8.1b) v1 = k1[H+][NO3-][HNO2] - k-1[NO2]2
(8.2a) NO2 + Fe(phen)32+ + H+ = HNO2 + Fe(phen)33+
(8.2b) v2 = k2[H+][ Fe(phen)32+][NO2] - k-2[HNO2][Fe(phen)33+]
(8.3) k1 = 0,9 (mol dm-3)-2min-1 (Orbán és Epstein, 1982)
(8.4) k-1 = 6,0 . 109 (mol dm-3)-1min-1 (Orbán és Epstein, 1982)
(8.5) k2 = 2,4.106 (mol dm-3)-2min-1
(8.6) k-2 = 1,2.103 (mol dm-3)-1min-1.
Erősen savas közegben a (8.0) reakció gyakorlatilag teljes, a (8.2) reakciót ennek megfelelően irreverzibilisnek tekintjük. A nagy felesleget figyelembe véve [H+] = [H+]0 jó közelítéssel teljesül. Ha a nitrogén-dioxidra kvázistacionárius állapotot tételezünk fel, és tekintetbe vesszük, hogy [NO3-]0 >> [Fe(phen)32+]0 miatt jó közelítéssel [NO3-] = [NO3-]0, a (8.0) reakció sebességét az
(8.7) r = (k1[H+]0[NO3-]0[HNO2][Fe(phen)32+]/(b + [Fe(phen)32+])
formulával adhatjuk meg. A
(8.8) b = 2k-1[NO2]ss/k2[H+]0
mennyiségről feltesszük, hogy állandó (ss a stacionárius koncentrációt jelöli). A KPP-tétel értelemszerű alkalmazásával a hullámsebességre a következőt kapjuk:
(8.9a) c* = 2(Dk1[H+]0[NO3-]0)1/2(s/(b + s))1/2
(8.9b) s = [Fe(phen)32+]0.
Amint a 8.1. ábra mutatja, (8.9) minőségileg helyesen helyesen írja le a mért sebesség-kezdeti koncentráció görbék alakját. (A kísérletekben a savasság biztosítására kénsavat használtunk.)
![[fig81.gif]](fig81.gif)
A c hullámsebesség függése a kezdeti koncentrációktól a nitrát-ferroin rendszerben. (a) ferroinfüggés, c/mm min-1 vs. 103([ferroin]0/mol dm-3); [NO3-]0 = 0,5; [H2SO4]0 = 3,5 mol dm-3. (b) Nitrátfüggés, c/mm min-1 vs. 10([NO3-]0/mol dm-3)1/2; [ferroin]0 = 5.10-3; [H2SO4]0 = 3,5 mol dm-3. (c) Savfüggés, c/mm min-1 vs. ([H+]0/mol dm-3)1/2; [NO3-]0 = 0,5; [ferroin]0 = 4.10-3 mol dm-3. Pontok: kísérleti értékek, vonalak: legkisebb négyzetes illesztéssel kapott értékek. (Póta, 1996)
Mivel a kísérletekben [Fe(phen)32+]0 >> b, a hullámsebesség gyakorlatilag független a ferroin kezdeti koncentrációjától. Legyen cinf a c*-[Fe(phen)32+]0 görbe határértéke, sb a c*-[NO3-]01/2 görbe meredeksége, sc pedig a c*-[H+]01/2 görbe meredeksége. Ha [H+] Hammett-féle savasságot jelent (Paul és Long, 1957) és a Dk1 mennyiséget - az egyszerűsítésekből származó hiba csökkentésére - illesztendő paraméternek tekintjük, akkor a (8.9) képlettel a kísérleti görbéket kvantitatíve is jellemezhetjük. A
(8.10) Dk1 = 1,16.10-2 mm2min-2(mol dm-3)-2
értékkel számított elméleti cinf, sb, sc mennyiségeket a kísérletiekkel való összevetésben mutatja a 8.1. táblázat.
| cinf /mm min-1 | sb /mm min-1(moldm-3)-1/2 | sc /mm min-1(moldm-3)-1/2 | |
| kísérleti | 1,06 | 1,24 | 0,16 |
| elméleti | 0,98 | 1,39 | 0,15 |
A hullámsebesség jellemzői a nitrát-ferroin rendszerben. cinf a c*-[Fe(phen)32+]0 görbe határértéke, sb a c*-[NO3-]01/2 görbe meredeksége, sc pedig a c*-[H+]01/2 görbe meredeksége.
A nitrát-ferroin reakcióban terjedő autokatalitikus hullám profilját úgy vizsgálhatjuk meg, hogy a reakcióelegyet tartalmazó küvettát alkalmas hullámhosszú fénnyel átvilágítjuk, videokamerával lefilmezzük, majd a felvételt számítógéppel kis cellákra osztjuk, és e cellákban meghatározzuk a feketedés mértékét. Megfelelő simítás, átlagolás és a standarddal való összevetés után így az adott hullámhosszon elnyelő komponens, például a ferroin térbeli koncentrációeloszlását kapjuk. A 8.2. ábrán a ferroin térbeli eloszlásának inflexiós pontbeli meredekségét (m) ábrázoltuk a kezdeti koncentrációk függvényében (Nagy és mtsai, 1991).
![[ferrprof.gif]](ferrprof.gif)
A hullámprofil inflexiós pontbeli meredeksége a kezdeti koncentrációk függvényeként a nitrát-ferroin rendszerben. (a) Ferroinfüggés, -103m/mol dm-3mm-1) vs. 103[ferroin]0/mol dm-3; [NO3-]0 = 0,5; [H2SO4]0 = 3,5 mol dm-3. (b) Nitrátfüggés, -103m/mol dm-3mm-1) vs. ([NO3-]0/mol dm-3)1/2; [ferroin]0 = 2.10-3; [H2SO4]0 = 3,5 mol dm-3. (c) Savfüggés, -103m/mol dm-3mm-1) vs. ([H+]0/mol dm-3)1/2; [NO3-]0 = 0,5; [ferroin]0 = 2.10-3 mol dm-3. Pontok: kísérleti értékek; vonalak: számított értékek. (Póta, 1996)
A korábbiakban megadott mechanizmusból m-re felírható, hogy
(8.11) m = A(k1/D)1/2[H+]01/2[NO3-]01/2[Fe(phen)32+]0.
Az A állandót a hullámprofilra vonatkozó egyenlet numerikus megoldásából lehet meghatározni, és kiderül, hogy a kísérletekben alkalmazott kezdetikoncentráció-tartományban - ahol [Fe(phen)32+]0 >> b - jó közelítéssel A = 0,36. A 8.2. ábrán látható folytonos egyeneseket (8.11)-ből számítottuk a szimultán legkisebb négyzetes illesztéssel (Valkó és Vajda, 1987) kapott
(8.12) k1/D = 4,7 (mol dm-3)-2mm-2
érték felhasználásával. A (8.10) és (8.12) egyenletekből külön-külön is meghatározhatjuk D és k1 értékét:
(8.13) k1 = 0,24 (mol dm-3)-2min-1; D = 8,4.10-6 cm2s-1.
Az irodalomban k1 (8.3)-beli értéke mellett D(ferroin) = 3,72.10-6 cm2s-1, D(ferriin) = 1,9.10-5 cm2s-1 (Ruff és Zimonyi, 1973) valamint az ionerősségtől függően D(salétromossav) = (0,71-2,2).10-5 cm2s-1 (Heckner és Scmid, 1971). Azt mondhatjuk tehát, hogy a hullámok vizsgálatából származó (8.13) értékek reális nagyságrendűek, s a nyert eredmények alátámasztják a reakció homogén rendszerbeli mérések alapján javasolt - itt felhasznált - mechanizmusát.
A salétromsav-vas(II) rendszerben az autokatalitikusan képződő salétromossav egy részét a vas(II) szubsztrátum időlegesen inaktív komplexbe viszi át (Bazsa, 1989). Megmutatható (Póta és mtsai, 1991), hogy ebben a rendszerben az autokatalitikus hullám terjedési sebessége jó közelítéssel
(8.14) c = 2(D[H+]0)1/2(k1[NO3-]0 - k3[Fe2+]0)1/2,
ahol k1 és k3 a kémiai mechanizmusból származó állandók, D pedig a salétromossav diffúziós együtthatója. Figyeljük meg, hogy már az autokatalizátor időleges elfogyása is tükröződik a sebességképletben, a ferroin szubsztrátum esetében is fellépő pozitív taghoz most egy negatív is társul. Természetesen az 1/2 kitevőjű hatványok alapjának pozitívnak kell lennie, ez kijelöli (8.14) érvényességi tartományát.
A salétromsav-hidroxil-amin rendszerben az autokatalitikusan képződő salétromossavat a mellékreakciók részben inaktív termékké alakítják, végleg eltávolítják a rendszerből. Az autokatalitikus hullám analitikus leírásakor (Jones és mtsai, 1994) a kísérletekkel összeegyeztethető
(8.15) c = 2D1/2(3k1/2 - k2[NH3OH+]0)1/2
formulához jutunk, amelyben a hidroxil-amin protonált formája szerepel, k1 és k3 pedig függ a savkoncentrációtól. Ha itt a zárójeles mennyiség nem pozitív, az azt jelenti, hogy az autokatalizátort fogyasztó reakciók túlsúlyban vannak, és valódi autokatalízis nem is alakul ki.
Az ismertetett esetekből kiderül, hogy a hullámsebesség egyszerű eszközökkel történő vizsgálatával következtetni lehet bizonyos kinetikai effektusokra (egy amerikai kutató találó kifejezése: "kinetics with a ruler" = "kinetika vonalzóval"). Ugyanakkor a módszernek vannak korlátai, például nem mindig tudjuk megállapítani, vajon az autokatalizátor időlegesen vagy véglegesen távozik-e el a rendszerből.
Ha az előzőekben bemutatott hullámokat viszonylag nagy átmérőjű csőben hozzuk létre úgy, hogy nem alkalmazunk pl. szilikagél vagy üvegpor töltetet, akkor a reakcióhő és a hidrodinamikai áramlások hatása erőteljessé válik. A hidrodinamikai áramlás következtében a hullámsebesség függhet például a reakcióelegyet tartalmazó cső gravitációs térhez viszonyított helyzetétől vagy attól, hogy a hullámot a cső alján vagy tetején keltjük-e. A gravitációs effektusok - az eltérő sűrűség- és a termikus viszonyok miatt - a vizsgált rendszer anyagi minőségétől függően más-más formában léphetnek fel (Bazsa és Epstein, l985; Nagypál és mtsai, l986). A töltött vagy paramágneses részecskék révén a villamos és mágneses tér ugyancsak befolyásolhatja a kémiai hullámok terjedési sebességét (Ortoleva, l987; Sevcikova és Marek, l986; Boga és Nagypál, l990a).
A Belouszov-Zsabotyinszkij-reakcióban a bromátionok erősen savas közegben szerves reagenseket oxidálnak, miközben brómozódás is lejátszódik; a folyamatot különféle fémionok katalizálják. A szerves reagens és a katalizátor minősége szerint számos változat ismeretes, egy, a hullámok vizsgálatában gyakori reakcióelegy összetétele H2SO4-BrO3--CH2(COOH)2-Ce(III)-Fe(phen)32+. A reakció alkalmas koncentrációviszonyok mellett oszcilláló sajátságú, azaz bizonyos anyagfajták koncentrációja a reakció során időben közel periodikusan változik. A teljes reakció számos egyidejűleg lejátszódó folyamatból tevődik össze, e folyamatok felderítése bonyolult. Ferroint tartalmazó reakcióelegyekben az oszcillációt magát egyszerűen észlelhetjük, mert az oldatban - a periodikus ferroin-ferriin átalakulásnak megfelelően - piros-kék színváltások lépnek fel. A mechanisztikus részleteket illetően Field és Burger (1985) munkájára utalunk.
A koncentrációgradiens hatására létrejövő ún. egydimenziós BZ-hullámokat Busse (1969) fedezte fel, aki a fentebb megadott összetételű reakcióelegybe felülről kénsavat cseppentve piros-kék sávrendszer kialakulását észlelte (9.1. ábra, a sávrendszer víz befecskendezésével is előállítható, ha az oldat már tartalmaz kénsavat).

Sav becseppentésével előállított, felfelé haladó sávrendszer a bromát-malonsav-Ce(III)-ferroin-kénsav elegyben. Balról jobbra haladva a felvételek időpontja a becseppentéstől számítva 60 s, 186 s, 285 s és 420 s. [bromát]0 = 0,07; [malonsav]0 = 0,3; [Ce(III)]0 = 0,0013 mol dm-3. A vízszintes fekete vonal a sav becseppentése után behúzott műanyagfólia, amely a küvettát kétfelé osztja.
A jelenség helyes magyarázata (Beck és Váradi, 1971, 1972; Beck, Váradi és Hauck, 1975) az, hogy bizonyos - a reakcióban részt vevő - anyagfajták koncentrációja befolyásolja az oszcilláció paramétereit (amplitudó, periódusidő); az x-tengely mentén létrehozott koncentrációgradiens hatására tehát az oszcilláció fázisban eltolva megy végbe e tengely mentén. A jelenségben a diffúziónak nincs lényeges szerepe, a sávvándorlás nem jár valódi anyagmozgással. Közvetlen kísérlettel kimutatható (Póta és mtsai, 1982), hogy ezek a hullámok átmennek az útjukba helyezett műanyagfólián. A szóban forgó hullámok tehát - bár kísérletileg mért sebességük nem állandó - fogalmilag megfelelnek a KPP-elméletben körvonalazott pszeudohullámoknak. A Belouszov-Zsabotyinszkij-reakcióban fellépnek olyan hullámok is, amelyek fogalmilag a KPP-elméletben körvonalazott trigger hullámoknak felelnek meg. Terjedésükhöz a diffúzió elengedhetetlenül szükséges, a terjedés mechanizmusa lényegében megfelel annak, amit az egyszerű autokatalitikus hullámoknál mutattunk be. A BZ-reakcióban a pszeudohullámok és trigger hullámok világos megkülönböztetése Winfree (1974) érdeme.
A katalizátorként ferroint tartalmazó elegyben egyetlen trigger hullám úgy kelthető, hogy a Petri-csészébe helyezett homogén elegy felszínének egy pontjához felhevített vagy ezüst-nitrát-oldatba mártott üvegbotot érintünk (Zsabotyinszkij, l974). Ekkor helyi inhomogenitás jön létre, amely kék körhullám formájában végigterjed a kétdimenziósnak tekinthető piros színű rendszeren. Ez a fajta hullám mind oszcilláló, mind pedig nem oszcilláló, hanem ún. gerjeszthető elegyben fellép. A gerjeszthetőség azt jelenti, hogy az időtől független nyugalmi állapotban lévő közeg nagy koncentráció-impulzus kibocsátásával reagál állapotának - egy küszöbértéket meghaladó - megzavarására; az impulzus lecsengése után a közeg egy ideig nem gerjeszthető újra, majd visszaáll a nyugalmi állapot, s a gerjesztés ismét lehetségessé válik (részletesebben lásd később).
A trigger hullámok sebességére elsőként Field és Noyes (1974) vezettek le kvantitatív képletet. Megfontolásaik szerint a haladó reakciófront előtti tartományban van valamennyi bromidion, amely a
(9.1a) BrO3- + Br- + 2H+ --> HBrO2 +HOBr
(9.1b) HBrO2 + Br- + H+ --> 2HOBr
egyenletek szerint elreagál, a HBrO2 koncentrációja igen alacsony értékre áll be, a keletkező HOBr pedig a malonsav brómozódására használódik el. Ugyanakkor a HBrO2 részt vesz a
(9.2a) BrO3- + HBrO2 + H+ --> 2BrO2. + H2O
(9.2b) BrO2. + Fe(II) + H+ --> HBrO2 + Fe(III)
(9.2c) 2HBrO2 --> BrO3- + HOBr + H+
reakciókban is, amelyekből az első kettő együttes hatásaként autokatalitikusan HBrO2 képződik, emellett pedig ferriin is keletkezik. A (9.1) és (9.2) reakciók vetélkedése szabja meg a hullámfront mozgását. A front mögött azután brómmalonsavból és ferriinből bromidionok képződnek, amelyek megállítják a HBrO2 autokatalitikus felszaporodását. A front előtt a bromidionok koncentrációja kicsiny, a front mögött viszont jóval nagyobb. Ez utóbbi, bromidionokban gazdag rétegbe nem hatolhat be újabb hullámfront addig, amíg a bromidionok koncentrációja (9.1) révén ismét le nem csökken. Ha feltesszük, hogy a hullám haladását döntően a HBrO2 (9.2a-b) szerinti autokatalitikus képződése szabja meg, és figyelembe vesszük, hogy a nagy felesleg miatt [H+] és [BrO3-] gyakorlatilag megegyezik a kezdeti értékével, akkor a
(9.3) v't = Dvvxx'' + k5[H+]0[BrO3-]0v
reakció-diffúzió egyenletet írhatjuk fel, ahol v = [HBRO2]. (A (9.2a-b folyamatban a BrO2. gyökre kvázistacionaritási feltételt alkalmaztunk, k5 az így kapott összetett reakció sebességi állandója.) A 4. pontbeli megfontolások alapján a (9.3)-hoz tartozó terjedési sebesség
(9.4) c = (4Dvk5[H+]0[BrO3-]0)1/2.
E levezetésnek - az erőteljes egyszerűsítések ellenére - jelentős igazságtartalma van. A trigger hullámok sebességét a BZ-reakcióban később még számosan vizsgálták, a különféle közelítéseket a 9.1. táblázat mutatja be.
| T/K | a/mm min-1 | b/mmmin-1dm3mol-1 | szerzők |
| 298 | -0,832 | 27,87 | Field és Noyes, 1974 |
| 298 | -1,957 | 25,86 | Showalter, 1981 |
| 291 | -3,2 | 28,3 | Wood és Ross, 1985 |
| 298 | -0,83 | 27,9 | Kuhnert és mtsai, 1985 |
| 298 | -3,43* | 58,34* | Sevcikova és Marek, 1983 |
Hullámsebesség a BZ-reakcióban, c = a + b([H2SO4]0[BrO3-]0)1/2. A mérések vékony oldatrétegben történtek, kivéve a * esetet, amely csőreaktorra vonatkozik (Vidal és Hanusse, 1986 nyomán).
A reakcióelegy viszkozitását - és így a diffúziós együtthatót - adalékanyagokkal megváltoztatva a hullámsebesség diffúziós együtthatótól való függése mérhető. A BZ-rendszerben végzett kísérletek négyzetgyökös függést szolgáltattak (Jorne, l980).
A Belouszov-Zsabotyinszkij-reakcióban fellépő, koncentrikus körhullámokból álló alakzatot (angolul: target pattern) a 9.2. ábra mutatja.
![[bzkorh.gif]](bzkorh.gif)
Koncentrikus körhullámok BZ-elegyet tartalmazó membránon, felülnézetből (videokamerával rögzítve, Károly Tamás, Gáspár Vilmos és Nagy István szívességéből, Póta (1996)).
E hullámok főbb sajátságai a következők (Zsabotyinszkij, l974):
- gerjeszthető vagy oszcilláló elegyben egyaránt létrejönnek;
- véletlenszerűen keletkeznek;
- különféle a periódusidejük (oszcilláló elegyben ez mindig más, mint az alapelegy periódusideje);
- a koncentrikus hullámok közül a legkülső sebessége a legnagyobb;
- a különböző hullámforrásokból kiinduló körhullámok találkozáskor megsemmisítik egymást, így elegendően hosszú idő múlva elvileg csak a legnagyobb frekvenciájú forrás fog létezni.
A hullámcentrumokban a közeg nyilvánvalóan oszcilláló és így bocsát ki koncentrikus körhullámokat. Egy-egy kör alakú kék hullámvonal kialakulásához valójában két hullám járul hozzá, először egy oxidáló hatású trigger hullám (kék), majd ezt követően - ahogyan az oxidált állapotú közeg visszatér eredeti állapotába - egy redukáló hatású trigger vagy pszeudohullám (piros) (Tyson és Fife, l980). A hullámcentrumbeli oszcilláció eredetéről röviden a következőt mondhatjuk (Tyson, l987): Az oszcillációt egyesek az oldatba hullott porszemcsék heterogén katalitikus hatására vezetik vissza. Ezt támasztja alá, hogy a hullámcentrumok periódusideje nem egyforma. Más elképzelések szerint a hullámcentrumok sajátos viselkedése azzal magyarázható, hogy a termikus koncentrációfluktuáció következtében a reakció lokálisan más kezdeti feltételek közé kerül mint amelyek az elegyben egyébként fennállnak, s a lokális oszcilláció ennek következtében jön létre. A következő kísérlet elvileg tisztázhatná a viszonyokat: fel kellene jegyezni egy bizonyos időpontig megjelent hullámforrások pontos helyét, majd a jelenlevő hullámcentrumok frekvenciájánál nagyobb frekvenciájú mesterséges hullámforrást kellene a rendszerben működtetni addig, amíg minden spontán hullámforrás eltűnne. Ezután abbahagyni a gerjesztést és megfigyelni, hol térnek vissza a spontán hullámforrások. Ha a hullámforrások az oldatba hullott porrészecskék miatt jönnnek létre, akkor eredeti helyükön kell újra megjelenniük, hiszen a mesterséges hullámforrás létrehozása a részecskék eredeti helyén elvileg mit sem változtatott. Ha a hullámforrások koncentrációfluktuációk révén jönnek létre, az új eloszlásuknak nem lehet köze az eredetihez. Megfelelő képrögzítéssel és statisztikai feldolgozással ezek az effektusok bizonnyal kimutathatók. A gyakorlatban természetesen e kísérlet megvalósításának sok buktatója van, ki kellene küszöbölni például a közeg konvekciós mozgását, amely az esetleges katalitikus részecskéket helyükről elmozdíthatná.
Érdekes kísérleti tény (Dockery és mtsai, 1988; Sevcikova és Marek, 1989), hogy a koncentrikus körhullámok sebessége függ a kibocsátó forrás frekvenciájától, azaz a fizikai hullámok diszperziójával analóg jelenség lép fel. Ennek a magyarázata az lehet, hogy egy adott hullám mindig az előző által hátrahagyott közegben terjed, s a terjedési sebessége függ attól, mennyire regenerálódott a közeg a megelőző hullám áthaladása után. Kézenfekvő, hogy nagy frekvencia esetén a közeg csak kevéssé képes regenerálódni, ami a sebesség csökkenésében mutatkozik meg.
A 9.3. ábrán látható spirális hullámokat kísérletileg úgy állíthatjuk elő, hogy a koncentrikus körhullámokat az elegy óvatos vízszintes mozgatásával vagy a körvonalra való óvatos ráfújással "elnyírjuk".
![[bzspir.gif]](bzspir.gif)
Spirális hullámok kialakulása a BZ-elegyben, felülről, (1), (2), (3) és (4) időben egymást követő fázisok (videokamerával felvéve, Károly Tamás és Nagy István szívességéből, Póta (1996)).
Az egymástól elválasztott hullámvégek egy idő múlva behajlanak és megkezdődik a spirálképződés. A spirális hullámok kialakulása jól követhető a gerjeszthető közeg egyszerűsített modelljében. Ebben feltételezzük, hogy a közeg egy pontjának háromféle állapota lehet: gerjesztett, refrakter és nyugalmi állapot. A gerjesztett pont Tg ideig marad ebben az állapotában, azután sorra átmegy a refrakter majd nyugalmi állapotba. A refrakter állapotban a pont Tr ideig van és ezalatt nem gerjeszthető. A 9.4. ábrán az előbbi állapotokat grafikusan ábrázoljuk.
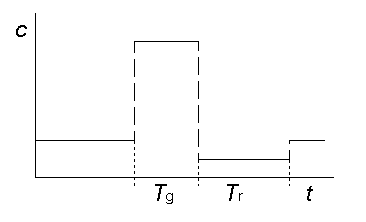
A gerjeszthető közeg egy pontjának időbeli viselkedése. Tg: gerjesztett állapot időtartama; Tr: a refrakter állapot időtartama.
Az egymással térbelileg szomszédos pontok egymásnak gerjesztést adhatnak át, ha egyikük gerjesztett, másikuk pedig nyugalmi állapotú. A 9.5. ábra alapján a spirálképződés könnyen követhető. Az ép hullámvonalat elnyírva a 0 fázishoz jutunk, amelyben a hullámvonal végeihez nyugalmi állapotokat tartalmazó közeg kerül a konvekció következtében. Ezután a gerjesztődés a hullám haladási irányára merőlegesen is megindul de a front környéke fáziselőnyben van; mindezek eredménye a spirálalak.
![[spirsim.gif]](spirsim.gif)
Spirális hullám szimulációja gerjeszthető elemek négyzetrácsán. Sötét: gerjesztett állapot, pontozott: refrakter állapot. A sötét vonal mindegyik esetben a hullámfront kiindulási helyzetét mutatja.Tg = 1, Tr = 2. A gerjesztett állapotú pontok minden lépésben gerjesztést adnak át a velük szomszédos, nyugalmi állapotú pontoknak, egy pontnak 8 szomszédja van. (Póta, 1996)
A kísérletek azt mutatják (Nagy-Ungvarai és mtsai, 1992a, b), hogy a kétdimenziós hullámfrontok terjedési sebessége a görbületüktől is függ. A haladási iránnyal ellentétesen görbülő hullámfront esetében a front normális sebessége kisebb a síkhullámnak megfelelő értéknél, míg a haladási irányba görbülő frontnál ellentétes hatás jelentkezik. Az intuitív magyarázat szerint ez azért van így, mert a terjedést segítő diffúzió az első esetben kevésbé, a második esetben pedig jobban érvényesül. Speciálisan a BZ-reakció esetében Keener és Tyson (1986) majd Tyson és Keener (1988) - igen színvonalas differenciálgeometriai eszközöket felhasználva - elméletileg részletesen vizsgálták ezeket a hatásokat, és levezették a gerjeszthető közegbeli hullámokra vonatkozó, nevezetes "eikonál"-egyenletet:
(9.5) N = c + DK,
ahol N a görbült hullámfront normális sebessége, c a síkhullám terjedési sebessége, D az autokatalitikus részecske diffúziós együtthatója, K pedig a front görbülete (a görbületi sugár reciproka). Megjegyzendő, hogy (9.5) meghatározott hibájú közelítés, amely jó eredménnyel a nagy görbületű frontoknál alkalmazható. A 9.6. ábra összefoglalja az elmondottakat.
![[gorbul.gif]](gorbul.gif)
Görbült hullámfrontok normális sebessége. (a) A haladási iránnyal ellentétesen görbülő front, a görbület (K) negatív, a normális sebesség csökken; (b) a haladási irányba görbülő front, a görbület (K) pozitív, a normális sebesség nő a síkhulláméhoz képest.
Ha az N és K mennyiségeket egy-egy konkrét esetben deriváltakkal felírjuk, (9.5) differenciálegyenletté alakul, amelyből a hullámfront alakját (például a spirál egyenletét) elvben meg lehet határozni. Az eikonál-egyenlet arra is alkalmas, hogy segítségével megbecsüljük, mekkora legyen az a térbeli perturbáció, amely stabilizálódó, kifelé induló körhullámot eredményez. Tanulságos számításokat találunk Tyson és Keener (1988) munkájában.
Igen pontos megfigyelések (Nagy-Ungvarai és mtsai, 1993) szerint a spirálhullámok végpontja a koncentrációviszonyoktól függően kör, ciklois vagy még bonyolultabb görbén mozoghat a hullám terjedése közben. A jelenséggel kapcsolatban intenzív kísérleti és elméleti munka vette kezdetét.
A háromdimenziós BZ-hullámok jellegzetes képviselői a tekercshullámok (angolul: scroll waves), amelyek a kétdimenziós koncentrikus körhullámok és spirálok háromdimenziós megfelelői. Ezek a hullámok vékony oldatrétegben lépnek fel, s egy ún. vezető szál (angolul: filament) körül helyezkednek el (Keener és Tyson, 1988, valamint a benne található referenciák). A 9.7. ábrán bemutatjuk az ún. tekercshullám-gyűrűt, a nyújtott spirálhullámokat valamint az ún. nyújtott koncentrikus hullámokat.
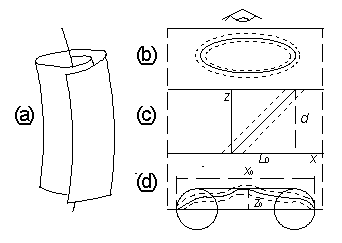
Háromdimenziós tekercshullámok. (a) Tekercshullám perspektivikusan. A vezető szál helyzete (b) tekercshullámból álló gyűrű; (c) nyújtott spirálhullám; (d) nyújtott koncentrikus hullámalakzat esetében. (Póta, 1996)
Az első esetben a vezető szál az oldatréteg belsejében zárt görbét alkot. A második esetben a vezető szál egyik vége az oldatréteg alsó lapján van, a másik vége pedig a felső lapra ér ki. A harmadik esetben a vezető szál mindkét vége az oldatrétegnek ugyanarra a lapjára támaszkodik. Az idő előrehaladtával a tekercshullám-gyűrűk zsugorodnak és végül eltűnnek, a nyújtott spirálok szimmetrikus formában stabilizálódnak, a nyújtott koncentrikus hullámok pedig szintén zsugorodnak és eltűnnek. Keener és Tyson (1988) a (9.5) egyenlethez hasonló mozgásegyenletet írtak fel a vezető szálra, s így sikerrel értelmezték a tekercshullámok időbeli evolúcióját. Ugyanakkor valószínű, hogy a BZ-rendszerekben még számíthatunk új, és meglepő hullámalakokra.
A stacionárius térbeli szerkezetek (anyagáramra nézve) nyitott rendszerben jöhetnek létre. Képzeljük el, hogy a vizsgált rendszerben térben homogén stacionárius állapot uralkodik, amely térben homogén perturbációkra stabilis. A legtöbb esetben a homogén stacionárius állapot térben inhomogén perturbációkra nézve is stabilis, ami azt jelenti, hogy a megzavarást leküzdve visszaállítja a homogén stacionárius állapotot. Előfordulhat azonban, hogy a homogén stacionárius állapot inhomogén perturbációkra nézve instabilis, és a rendszer a homogén stacionárius állapotból egy stabilis, ám inhomogén stacionárius állapotba megy át. A homogén stacionárius állapot stabilitási viszonyait legegyszerűbben lineáris közelítésben vizsgálhatjuk meg. Tekintsük az
(10.1a) u't = Duuxx'' + f(u, v)
(10.1b) v't = Dvvxx'' + g(u, v)
rendszert, ahol f és g jellemzik a rendszerben lejátszódó kémiai reakciók anyagtermelését. Írjuk be a (10.1) rendszerbe az
(10.2a) u(x, t) = u0 + A exp(pt+ikx)
(10.2b) v(x, t) = v0 + B exp(pt+ikx)
alakú perturbációkat, ahol (u0, v0) (10.1) stacionárius állapota, i pedig a képzetes egység. Ha feltesszük, hogy a stacionárius állapottól való eltérés kicsiny, f és g (u0, v0) körüli sorbafejtésével az A és B együtthatókat lineáris, homogén egyenletrendszerből határozhatjuk meg. Az ilyen rendszereknek akkor van nemtriviális megoldásuk, ha determinánsuk eltűnik. Ebből a feltételből meghatározhatjuk, hogy milyen k hullámszámú ( 2pi/k hullámhosszú) perturbációkra lesz p pozitív, azaz milyen perturbációk erősödhetnek fel. Vezessük be a következő jelöléseket:
(10.3a) a11 = f'u(u0, v0); a12 = f'v(u0, v0);
(10.3b) a21 = g'u(u0, v0); a22 = g'v(u0, v0)
továbbá
(10.4a) s0 = a11 + a22
(10.4b) d0 = a11a22 - a12a21
(10.4c) s = s0 - (Du + Dv)k2
(10.4d) d = d0 - (a11Dv + a22Du)k2 + DuDvk4.
Tételezzük fel, hogy diffúzió hiányában a homogén stacionárius állapot stabilis, azaz
(10.5) s0 < 0 és d0 > 0
teljesül. Egyszerű számolással kapjuk, hogy p > 0 szükséges és elégséges feltétele a következő:
(10.6a) a11Dv + a22Du > 0 és
(10.6b) (a11Dv + a22Du)2 - 4DuDvd0 >0.
Ha (10.6) teljesül, akkor a d = 0 egyenletnek k2-re két pozitív gyöke van, s mindazok a perturbációk, amelyeknél a hullámszám négyzete e két gyök közé esik, felerősödnek.
Véges térbeli kiterjedésű rendszerekben ugyanakkor a lehetséges hullámszámoknak eleget kell tenniük a peremfeltételeknek is.
Ha az adott kezdeti eloszlásból kialakuló stacionárius térbeli szerkezetekről a lineáris közelítésen túlmenő információkat kívánunk szerezni, közvetlenül meg kell oldanunk - megfelelő kezdeti és peremfeltételek mellett - a (10.1) rendszert. Ha a lehetséges stacionárius állapotokat kívánjuk pontosan meghatározni, akkor (10.1) bal oldalát zérussá tesszük, s az így kapott közönséges differenciálegyenlet-rendszert oldjuk meg, megfelelő peremfeltételek mellett. Mindig célszerű azonban előzetes tájékozódásként elvégezni a lineáris stabilitásvizsgálatot.
A stacionárius térbeli szerkezetek elméletének létrehozásában fontos szerepet játszott Turing (1952), aki a számítógépekkel kapcsolatos munkája mellett a morfogenezis által motivált, úttörő jelentőségű dolgozatot írt. Azóta számos elméleti-matematikai eredmény született e területen, itt csupán Edelstein-Keshet (1988) és Murray (1993) könyveit említjük meg.
Noszticzius és mtsai (1987) alkották meg az első folytonosan táplált, nem kevert "hullámreaktort" (CFUR= continuously fed unstirred reactor), s ezzel nagymértékben hozzájárultak a stacionárius térbeli szerkezetek kísérleti felkutatásához. Castets és mtsai (1990) mintegy 40 évvel Turing elméleti munkája után stacionárius térbeli szerkezeteket fedeztek fel a klorit-jodid-malonsav-reakcióban. (Az angol CIMA = chlorite-iodide-malonic acid betűszót gyakran használjuk e reakció jelölésére.) A CIMA-reakcióban kialakuló szerkezetek első modellje Lengyel és Epstein (1991) nevéhez fűződik. A CIMA-reakcióban jód keletkezik, ami jodidionok jelenlétében keményítővel kék színt ad, s az így kialakuló színtelen-kék mintázat vizuálisan észlelhető a nem kevert, térbeli reaktorban. Ouyang és Swinney (1991) már kvázi-kétdimenziós elrendezésben vizsgálták a CIMA-reakcióban fellépő szerkezeteket, s a kezdeti feltételektől és paraméterektől függően több, eltérő szimmetrájú mintázatot észleltek. Rendkívül érdekes, hogy a hőmérséklet változtatásával is változott a mintázat szimmetriája, és 18 0C alatti hőmérsékleten mindig a lúdbőrhöz hasonló szerkezet lépett fel.
Murray (1993) részletesen ismerteti könyvében az emlősök bundázatában található foltok és sávok kialakulására vonatkozó - az első közlés óta igen nevezetessé vált - elméletét. Az elmélet kiindulópontja az, hogy a bunda későbbi mintázatát még az embrionális szakaszban megszabó "morfogén" reakció-diffúzió mechanizmussal terjed szét az embrió felületén, és stacionárius eloszlás alakul ki. A számítások során kiderült, hogy az embrió méretének növekedtével a mintázat jellege nagymértékben változik: a kis állatok kicsiny embrióin nincs mintázat, majd a fehér-fekete és fekete-fehér-fekete mintázatú állatok következnek; a méret további növekedtével a ragadozók jól ismert foltos-sávos bundáját kapjuk, végül az egészen nagy állatokon olyan sűrű mintázat alakul ki, amely már egybeolvad és az állat egyszínűnek látszik. A 10.1. ábra vázlatosan mutatja az eredményeket.
![[mur.gif]](mur.gif)
Murray számítási eredményei vázlatosan: (a) kis állatok, nincs mintázatuk; (b) Mellivora capensis, Capra aegagrus hircus; (c) Tamandua tetradactyl; (d) foltos bundájú macskafélék (e) nagy állatok, kivehetetlenül sűrű, egybefolyó mintázat. (Póta, 1996)
Murray érdekes tapasztalata, hogy a mintázat jellege szempontjából kevéssé érdekes, pontosan milyen reakció-diffúzió egyenleteket használunk a számításokhoz, feltéve, hogy azok képesek stacionárius térbeli szerkezeteket produkálni. Így tehát még az sincs kizárva, hogy a különféle állatok mintázatait ugyanaz a kémiai-biológiai mechanizmus hozza létre.
A kémiai hullámokra vonatkozó vizsgálatok várhatóan a jövőben is tovább folynak. Érdemes talán megvizsgálni (Arnold és Showalter, l987) mekkora az a legnagyobb hullámsebesség, amely oldatokban elképzelhető és mérhető. Mivel a diffúziókontrollált folyamatokra k ~ 1010 M-1 s-1, a diffúziós együttható tipikus értéke pedig D ~ 10-5 cm2 s-1, a (4.4) formula u0 = 0,25 M esetében a c~10 ms-1 sebességet szolgáltatja. Nagyjából ennyi a férfi 100 m-es síkfutás világcsúcs körüli futójának átlagsebessége is. A jelenleg ismert hullámsebességek viszont ennek az értéknek csupán kb. tízezred részét érik el. Nem valószínű, hogy az előzőekben megbecsült sebesség a gyakorlatban is mérhető lenne. Ehhez először is vagy nagyon finom időmérő eszköz, vagy nagyon hosszú cső kellene. Komolyabb ellenvetés azonban az, hogy az autokatalizátor nyomokban rendszerint jelen van a reakcióhoz használt vegyszerek legalább egyikében, így valójában a hullámvezető cső teljes hosszában egyidejűleg folyik az autokatalitikus reakció. A kis sebességű reakcióknál ez a spontán reakció sokáig nem vehető észre, a mesterségesen keltett hullám szabadon terjedhet. Gyors reakció esetében azonban a rendszer eléggé hamar "berobban" és elfedi a terjedő reakciófrontot, amely addig mindössze néhány mm távolságot tett meg. Valószínűleg a spontán kémiai reakció okozza, hogy némely front sebessége elegendő hosszú idő múlva gyorsulónak mutatkozik.
Manapság talán a hullámprofil kísérletes meghatározása, a gyorsuló hullámok és a Turing-féle szerkezetek vizsgálata nyújtja a legvonzóbb feladatokat. A többdimenziós spektrofotometria, digitális képrögzítés és feldolgozás (Müller és mtsai, l986) a kísérleti technika számára új távlatokat kínál. A periodikusan irányt váltó, "visszaverődő", és felhasadó hullámok (Kawczynski, 1983; Röhricht és Horsthemke, 1991; Petrov és mtsai, 1994) kísérletes megvalósítása és vizsgálata is nagyon érdekes kutatási cél lehet.
Míg korábban a kémiai hullámok vizsgálatában a hidrodinamikai áramlások kiküszöbölése volt a cél, ma többen törekszenek arra, hogy jól meghatározható hidrodinamikai jelenségek valamint a kémiai reakciók összekapcsolása révén minőségileg új térbeli szerkezeteket hozzanak létre.
A kémiai hullámok példáján jól tanulmányozhatók az egyébként is fontos csatolási jelenségek (Gáspár és mtsai, 1991; Tóth és mtsai, 1994). Biológiai jelentősége is lehet a kémiai hullám labirintusbeli útkereső sajátságának (Steinbock és mtsai, 1995).
Mindez - az itt nem említett biológiai tárgyú munkákkal együtt - ma még be nem látható távlatokat nyit a több tudományágat sajátos módon egyesítő térbeli nemlineáris dinamika számára.
Arnold, R and Showalter, K.: J. Chem. Educ. 64, 740 (1987), Translator's Comment 3.
Bazsa, G. and Epstein, I.R.: J. Phys. Chem. 89, 3050 (1985).
Bazsa, G.: Kémiai Közlemények 68, l50 (1987-88).
Bazsa, G: D. Sc. Thesis, Debrecen, 1989.
Beck, M. and Váradi, Z.: Magyar Kém. Foly. 77, l67 (197l).
Beck, M.; Váradi, Z. and Hauck, K.: Magyar Kém. Foly. 8l, 86 (1975).
Beck, M.T. and Váradi, Z.B.: Nature 235, l5 (1972).
Belouszov, B.P.: Szb. Refer. po Radiac. Medicine za 1958 g., Medgiz, Moszkva 1959, sztr. l45.
Boga, E.; Kádár, S.; Peintler, G.; Nagypál, I.: Nature 347, 749 (1990)
Boga, E.; Peintler, G. and Nagypál, I.: J. Am. Chem. Soc. 112, 151 (1990). (a)
Busse, H.G.: J. Phys. Chem. 63, 750 (1969).
Castets, V.; Dulos, F.; Boissonade, J. and De Kepper, P.: Phys. Rev. L. 64, 2953 (1990).
De Kepper, P.; Epstein, I.R.; Kustin, K. and Orbán, M.: J. Phys. Chem. 86, l70 (1982).
Dockery, J. D.; Keener, J. P.; Tyson, J.J.: Physica 30D, 177 (1988).
Edelstein-Keshet, L.: Mathematical Models in Biology, Random House, New York, 1988.
Epik, P.A.; Sub, N.Sz.: Dokl. Akad. Nauk SzSzSzR, 100, 503 (1955).
Epstein, I.R.; Kustin, K. and Warshaw, L.J.: J. Am. Chem. Soc. 102, 375 (1980).
Field, R.J. and Noyes, R.M.: J. Am. Chem. Soc. 96, 2001 (1974).
Field, R.J.; Burger, M. (Eds): Oscillations and Traveling Waves in Chemical Systems, Wiley, New York, 1985.
Fife, P.C.: Mathematical Aspects of Reacting and Diffusing Systems, Lecture Notes in Biomathematics 28, Springer-Verlag, Berlin-Heidelberg-New York 1979.
Fisher, R. A.: Ann. Eugenics 7, 355 (1937).
Furrow, S.: J. Phys. Chem. 9l, l707 (1987).
Gáspár, V.; Maselko, J.; Showalter, K.: Chaos 1, 435 (1991).
Gear, C.W.: Numerical Initial Value Problems in Ordinary Differential Equations, Prentice-Hall, Englewood Cliffs 197l.
Gowland, R.J. and Stedman, G.: J. Chem. Soc. Chem. Commun. l038 (1983).
Gowland, R.J.; Jones, E. and Stedman, G.: React. Kinet. Catal. Lett. 32, l5 (1986).
Gray, P.; Showalter, K. and Scott, S.K.: J. Chim. Phys. 84, l329 (1987).
Gribschaw, T.; Showalter, K.; Banville, D.L. and Epstein, I.R.: J. Phys. Chem., 85, 2l52 (198l).
Hanna, A.; Saul, A. and Showalter, K.: J. Am. Chem. Soc. l04, 3838 (1982).
Harrison, J. and Showalter, K.: J. Am. Chem. Soc. l08, 225 (1986).
Heckner, H. N.; Schmid, G.: Electrochim. Acta 16, 131 (1971).
Jones, E.; Póta, G.; Stedman, G.: Catalysis Letters 24, 211 (1994).
Jones, E.; Póta, G; Stedman, G.: Catalysis Letters 24, 211 (1994).
Jorne, J.: J. Am. Chem. Soc. l02, 6196 (1980).
Kaliappan, P.: Physica 11D, 368 (1984).
Kaps, P and Rentrop, P.: Numer. Math. 33, 55 (1979).
Kawczynski, A. L.: Polish J. Chem. 57, 1323 (1983).
Keener, J. P.; Tyson, J. J.: Physica 21D, 307 (1986).
Keener, J.P. and Tyson, J.J.: Science 239, l284 (1988).
Kolmogorov, A.N.; Petrovszkij, I.G.; Piszkunov, N. Sz.: Bjul. MGU, Matematika i mehanika, l(6), l (1937).
Kubicek, M.; Marek, M.: Computational Methods in Bifurcation Theory and Dissipative Structures, Springer-Verlag, New York-Berlin-Heidelberg-Tokyo 1983.
Kuhnert, L.; Krug, H.J.; Pohlmann, L.: J. Phys. Chem. 89, 2022 (1985).
Lee, K. J.; McCormick, W. D.; Ouyang, Q.; Swinney, H. L.: Science Wash. 261, 192 (1993).
Lengyel, I.; Barna, T.; Bazsa, G.: J. Chem. Soc. Faraday Trans. l, 84, 229 (1988).
Lengyel, I.; Epstein, I. R.: Science 251, 650 (1991).
Luther, R.: J. Chem. Educ. 64, 740 (1987), (English translation).
Luther, R.: Z. Electrochem. l2, 596 (1906).
Merkin, J.H.; Needham, D.J.; Scott, S.K.: Proc. Roy. Soc. Lond. 424A, l87 (1989).
Murray, J.D.: Lectures on Nonlinear-Differential-Equation Models in Biology, Clarendon Press, Oxford 1977.
Murray, J.D.: Mathematical Biology, 2nd Ed., Springer, Berlin-Heidelberg, 1993.
Müller, S.C.; Plesser, T.; Hess, B.: Naturwissenschaften 73, 165 (1986).
Nagy, I. P.; Póta, G.; Bazsa, G: J. Chem. Soc. Faraday Trans. 87, 3613 (1991).
Nagy-Ungvarai, Zs.; Pertsov, A. M.; Hess, B.; Müller, S. C.: Physica 61D, 205 (1992) (a)
Nagy-Ungvarai, Zs.; Ungvarai, J.; Müller, S. C.: Chaos 3, 15 (1993).
Nagy-Ungvarai, Zs.; Ungvarai, J.; Müller, S. C; Hess, B.: J. Chem. Phys. 97, 1004 (1992). (b)
Nagypál, I.; Bazsa, G.; Epstein, I.R.: J. Am. Chem. Soc. 108, 3635 (1986).
Nicolis, G and Prigogine, I.: Self-Organization in Nonequilibrium Systems, Wiley, New York 1978.
Noszticzius, Z.; Ouyang, Q.; McCormick,W. D.; Swinney, H. L.; Tam, W. Y.: Nature 329, 619 (1987).
Orbán, M.; Epstein, I.R.: J. Am. Chem. Soc. 104, 59l8 (1982).
Ortoleva, P.: Physica 26D, 67 (1987).
Ouyang, Q; Swinney, H.: Nature 352, 610 (1991).
Paul, M.A.; Long, F.A.: Chem. Rev. 57, 1 (1957).
Petrov, V.; Scott, S. K.; Showalter, K.: Phil. Trans. R. Soc. Lond. A 347, 631 (1994).
Póta, G.; Bazsa, G.; Beck, M.T.: Acta Chim. Acad. Sci. Hung. 110, 277 (1982).
Póta, G.; Lengyel, I.; Bazsa, G.: J. Chem. Soc. Faraday Trans 1, 85, 3871 (1989).
Póta, G.; Lengyel, I.; Bazsa, G.: J. Phys. Chem. 95, 4379 (1991).
Póta Gy.: Kémiai hullámok és térbeli szerkezetek reakció-diffúzió rendszerekben, egyetemi jegyzet, Kossuth Egyetemi Kiadó, Debrecen 1996.
Rastogi, R.P.; Varma, M.K.; Yadava, R.D.; Singh, K.S.: J. Chem. Soc. Faraday Trans. 1, 81, 751 (1985).
Reusser, E.J.; Field, R.J.: J. Am. Chem. Soc. 101, 1063 (1979).
Röhricht, B.; Horsthemke, W.: Preprint, 1991.
Rudakov, E.Sz.; Masztihin, V.M.; Popov, S.G.; Rudakova, R.I.: Org. Magn. Reson. 5, 343 (1973).
Ruff, I.; Zimonyi, M.: Magyar Kém. Foly. 79, 135 (1973).
Schubert A.: Homogén reakciók kinetikája, MK, Budapest 1976.
Sevcikova, H.; Marek, M.( Physica 21D, 61 (1986).
Sevcikova, H.; Marek, M: Physica 9D, 140 (1983).
Sevcikova, H; Marek, M.: Physica 39D, 15 (1989).
Showalter, K.; Tyson, J.J.: J. Chem. Educ. 64, 742 (1987).
Showalter, K: J. Phys. Chem. 85, 440 (1981).
Steinbock, O; Tóth, Á.; Showalter, K.: Science 267, 868 (1995).
Szirovicza, L.; Nagypál, I.; Boga, E.: J. Am. Chem. Soc. 111, 2842 (1989).
Tóth, Á.; Gáspár, V.; Showalter, K.: J. Phys. Chem. 98, 522 (1994).
Turing, A.: Philos. Trans. R. Soc. London B 327, 37 (1952).
Tyson, J.J. and Keener, J.P.: Physica 29D, 215 (1987).
Tyson, J.J. and Keener, J.P.: Physica 32D, 327 (1988).
Tyson, J.J.: J. Chim. Phys. 84, 1359 (1987).
Tyson, J.J.; Fife, P.C.: J. Chem. Phys. 73, 2224 (1980).
Valkó P.; Vajda S: Műszaki-tudományos feladatok megoldása személyi számítógéppel, MK, Bp. 1987.
Váradi, Z.B.; Beck, M.T.: BioSystems 7, 77 (1975).
Vidal, C.; Hanusse, P.: Int. Rev. Phys. Chem. 55, l (1986).
Weitz, D.M.; Epstein, I.R.: J. Phys. Chem. 88, 5300 (1984).
Welsh, B.J.; Gomatam, J.: Physica 43D, 304 (1990).
Winfree, A.T.: Faraday Symp. Chem. Soc. 9, 43 (1974).
Winfree, A.T.: Science 181, 937 (1973).
Wood, P.M.; Ross, J.: J. Chem. Phys. 82, 1924 (1985).
Zhabotinsky, A.M.; Rovinsky, A.B.: J. Phys. Chem. 94, 8001 (1990).
Zsabotyinszkij, A.M.: Koncentracionnüe avtokolebányija, Nauka, Moszkva 1974.
A Centre for Nonlinear Sciences, University of Leeds honlapjáról tájékozatást kapunk bizonyos interdiszciplináris kutatásokról a nemlineáris dinamika terén, az intézmény által szervezett kurzusokkal, idevágó konferenciákkal együtt. Ismertetés található itt az intézménnyel kapcsolatban álló szakfolyóiratokról (például Physica D, Physics Letters A), és hozzáférhető az intézmény saját Internet folyóirata, a Nonlinear News is.
John Pojman a konvekciós és polimerizációs kémiai hullámok ismert kutatója (University of Southern Mississippi, USA), honlapja aktuális kutatásait mutatja be. Érdemes információt kérni tőle az általa beindított nemlineáris témájú list server-ről, ahol a tagok által e-mail-en beküldött információt minden tag megkapja.
A School of Chemistry, University of Leeds címen többek között megtaláljuk S. K. Scott-nak, a nemlineáris kémiai dinamika ismert kutatójának, több világszerte kapható könyv szerzőjének honlapját aktuális kutatásaival és publikációival.
A Software for Nonlinear Dynamics címen a Darmstadt-i egyetem elméleti fizikai tanszékének letölthető szoftverválasztékát találjuk. A programok többsége a káosszal kapcsolatos mennyiségek számítására szolgál. A cím inkább napközben érhető el.
A Nonlinear Chemical DynamicsGroup, West Virginia University címen K. Showalter, a nemlineáris kémiai dinamika egyik vezető kutatója által irányított csoport honlapját találjuk publikációkkal, a hullámokra vonatkozó képanyaggal együtt.
A Nonlinear Dynamics Network, Prague cím a nemlineáris kémiai dinamika európai iskoláit igyekszik összefogni, még szervezés alatt áll.
A Centre for Nonlinear Phenomena and Complex Systems, Univ. Libre,Brussels az irreverzibilis termodinamika nagy alakja, a Nobel-díjas I. Prigogine munkássága nyomán fejlődött nagy tekintélyű kutatóhellyé. A címen az intézet személyzetének bemutatása, az aktuális kutatások leírása szerepel.