COMPUTER and MULTIMEDIA TOOLS
for ENGINEERS and SCIENTISTS
using or teaching APPLIED MATHEMATICS
Láng-Lázi, M.,(*) Kollár-Hunek, K.,
Viczián, Zs., Donáth, K.(**) Technical University Budapest,
(*) Inst. of Mathematics, (**) Dept. of Chemical Information Technology
e-mail: lazi@ch.bme.hu
Abstract
Computer aided mathematical calculations, design, qualified data banks
and quality assurance have become a very important part in the education
of engineers. At the end of the 20-th century this importance implies the
using of the best SOFTWARE and the best tools of information technology
that are available for teaching and research. The paper presented summarizes
the experiences of using computers in the basic mathematical and some advanced
(Ph.D. or voluntary student research) courses at the Chemical Engineering
Faculty of the Technical University Budapest (TUB) and at the Brevard Community
College (BCC, FL, USA). A new way of teaching is given by the MULTIMEDIA.
One of the authors has been a popular instructor of a special TV course
in Statistics of the Quality Assurance direction for three terms in the
USA. We show the specialities of this telecourse, too, and the possibilities
of its transfer to the Hungarian education .
Introduction
Mathematics is one of the most important - or perhaps the most important
- base of the engineering sciences. If the students have terrible difficulties
in understanding and using the algebraic steps or the methods of the calculus
they will be burdened in every level in their studies and this fact doesn't
depend on their later specialization - whether they will be studying Analytical
Chemistry, Mechanics, Reactionkinetics, Quality Assurance , Chemical, Mechanical,
Electrical or Civil Engineering, perhaps Transportation. In every subject
of their special field they have to use either differentiation and integration
or statistical methods to analyse errors or confidence - and all of this
is full of algebraic and also computational steps. Now, at the end of the
20th century we have to change our way of teaching and applying Mathematics
in Engineering - it means we not only have to make its theoretical parts
understandable - but we also ought to teach the students how to find the
available formal and applied mathematical software on the netware, to develop
the ability in the students to use these tools.
Computer Algebra: PLATO? DERIVE? MAPLE? or...?
PLATO Courseware has been designed by the Computer-Based Training
and Education Company: TRO Learning, Inc.(4660 West 77th Street, Edina,
Minnesota 55436, USA) for skill development with real life applications
in several fields. (Table 1.)
Table 1. Moduls of PLATO
| Modul |
No. of SM |
Lab. Hours / Objectives in a SubModul |
| Communication |
5 |
139/466 ; 40/134 ; 122/455 ; 60/112 ; open/100 |
| Mathematics |
10 |
95/671 ; 23/177 ; 36/298 ; 20/136 ; 27/75 ; 10/78 ; 45/156 ; 16/36
; 38/182 ; 36/164 |
| Science |
5 |
42/869 ; 48/135 ; 40/38 ; 35/92 ; 21/99 |
| Social Studies |
1 |
40/318 |
| Technology |
2 |
9/26 ; open ended |
| Life Skills |
3 |
30/119 ; 15/65 ; 6/30 |
| Technical Skills |
7 |
6/25 ; 20/83 ; 290/391 ; 54/63 ; 37/49 ; 40/37 ; 20/44 |
| PLATO Workskills |
4 |
29/72 ; 39/132 ; 42/79 ; 24/61 |
One of the authors was using at BCC (FL/USA) the modul Mathematics in
the courses Preparative Algebra (College credit-prerequisit course) and
Calculus 2. with Analytical Geometry (University and College credit course).
In Table 2. we are showing the submoduls of Mathematics used in the Calculus
university-credit course.
Table 2. PLATO submoduls in Mathematics used in Calculus
| Submodul |
Number of Chapters |
Used Chapters |
Used Objectives |
| Advanced Algebra |
5 |
Coordinates and curves |
Parabolas, Ellipses and Hyperbolas |
| Calculus 2 |
17 |
L'Hospital's Rule |
L. H. rule ; Further Indeterminate Forms |
|
|
Numerical Integration |
Trapezoidal and Simpson's Rule |
|
|
Improper Integrals |
Improper Integrals |
|
|
Lengths of Curves |
Lengths of Curves |
|
|
Sequences |
Sequences, Taylor's Theorem |
|
|
Series |
Introduction, Results on Infinite Series |
Corresponding to our experiences the most effective way of using
PLATO in Mathematics is to use the TUTORIAL part by every student
and after having it completed to offer a choice to the students: to continue
by the TEST part of PLATO, to write a usual paper-pencil
test or to start with the more advanced DERIVE software. As an example
we are showing a small part (about 10% of a one-hour lab.) of a PLATO
-TUTORIAL and the corresponding DERIVE exercise:
1. PLATO: Given is the equation: (y+3)2/64 - (x-1)2/9
= 1
| Determine whether the hyperbola |
opens up and down |
or |
left and right |
| Find the coordinates of the vertices and foci |
V1( , ) V2( , ) |
|
F1( , ) F2( , ) |
When the correct answer is given the PLATO TUTORIAL responds
by the graph of the equation labelling the asked points.
2. DERIVE: Sketch the graph of the conic section given by the
equation: 9x2 + 12xy + 4 y2 + 2x - 3y = 0.
| The angle of rotation is: |
1/2arctan[b/(a-c)]= |
The asymptotes are:
(Plot them!) |
|
As we see DERIVE needs more independent imagination. After a
certain level of knowledges it is more effective than PLATO.
The software DERIVE is a very flexible tool at every level of
teaching and using Mathematics. As we have shown DERIVE can be used
just after learning the first basic sections in Analytical Geometry or
in Algebra. It is a real "Easy to Use" software and in its further
possibilities DERIVE can be applied in some Ph.D. courses or even
in research work, as well. (Berry and Mason 1993) Another advantage we
have to mention is the velocity of DERIVE. In the Calculus textbook
of Zill (1992) for a certain integral the given computation time of the
MATHEMATICA software is about three times as much as the same integral
needs by DERIVE. We had similar experiences comparing MAPLE
and DERIVE in a numerical problem of our research - a surface fitting
where we had to solve a parametric linear system with 15 unknowns.
The complex system in teaching and applying Mathematics and Informatics
At TU Budapest we use Computer Algebra and other software for Numerical
Analysis in the undergraduate (B.Sc.), graduate (M.Sc.) and postgraduate
(Ph.D.) courses as well. Our system is the following: We have a team with
co-workers from several departments of the Chemical Engineering Faculty
and of the Institute of Mathematics. The Dept. of Chemical Information
Technology and the Dept. of Analysis in the Inst. of Mathematics are responsible
for the courses on Computing and Mathematics at the Chemical Engineering
Faculty. They offer some Ph.D. courses in Computing and Numerical Analysis
so that one part of these courses consists of traditional lectures, the
second part is the solution of a numerical analysis problem given by the
research work of the Ph.D. student and the third part of these courses
is teaching - the Ph.D. students teach in the undergraduate Computing or
Computational Mathematics courses and usually they develop one or two new
exercises for the M.Sc. courses, as well.
In this complex system our Ph.D. students have the chance to choose
any software from the available DERIVE, MAPLE, MATHEMATICA, perhaps
the older NUMBOX or for some special problems in mechanical engineering
the MATHCAD, for the solution of their own research-problem. They
have the same freedom in developing new exercises or new software for the
M.Sc. courses.
We have utilized the experiences of our Ph.D. students in small-group-classes
(12-24 students/group) of the regular B.Sc. courses in Mathematics and
Computing. We have developed a very effective contact between these classes,
that is for all first-year-students (about 250) a COMPUTER-SHOW
was held in Mathematics after the chapters Differentiation, Sketching graphs
of functions, Taylor expansion, Determinants, Matrices using the possibilities
of MULTIMEDIA. Thereafter in the small-groups as a part of their
Computing classes the students prepared a WINWORD document for the
mathematical formulas and inserted their own developed DERIVE graphs
or EXCEL tables and graphs in these documents. The advantages of
this computer-supported-Mathematics were obvious at every level, first
of all in the English courses of the TUB and in the Calculus 1-2 courses
of the BCC Florida. The reason of the evident effectivness in the latter
two courses is the fact that the students enrolling in these courses come
with very different levels of knowledge, so they really need to face what
they learn in theory .
In Table 3. we are showing the area of Ph.D. exam-works (Numerical Analysis)
or voluntary student research (TDK) workers in Chemical Engineering, Mechanical
Engineering Physical Chemistry, Physics and directly in Information Technology.
Table 3. TDK and Ph.D. exam works
(Num. Analysis and Information Techn.)
| Title |
Num. Methods used |
Software |
Characteristics of complex
hydrocarbon mixtures |
Roots of Equations
Numerical Integration
Spline
FittingDifferentiation |
DERIVE
MATHEMATICA |
Velocity distribution and
flow zones in a conical hopper |
Num. Solution of O.D.E.-s
Extrema of Functions
Curve Fitting (Polynomial) |
DERIVE
MATHCAD
NUMBOX |
Ternary Vapour-Liquid Equilibrium
calculations |
Num. Solution of P.D.E.
Surface Fitting
Lin Algebra |
DERIVE
MAPLE
own PASCAL pr. |
Computer implementation of
polarographic analytical method |
Line Fitting
Extrema of Functions |
own programs
and Macros |
Stability of dynamical systems
(a bifurcation-problem) |
Num. Solution of O.D.E-s
Critical Points of Functions
Depending on 2 Variables
Num. Methods of Lin. Algebra |
DERIVE
own PASCAL
program |
One may ask what is the reason of developing a program of our own when
a wide scale of excellent and even not very expensive software is available
nowadays.
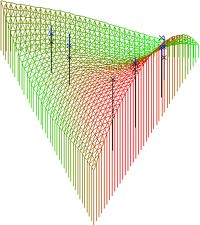 As a
very interesting example we show first the quite simple problem of ternary
equilibrium pressure-surfaces. The so called triangle-diagrams are as well-known
in Chemistry as in Mathematics the C' surfaces over the basic R2
simplex. But there is not any graphic software available that can plot
a surface over a non-rectangular region. In this figure we are showing
the graphic result of our own PASCAL program where one can obviously see
the binary pressure curves: the boundaries of the ternary pressure surface.
As a
very interesting example we show first the quite simple problem of ternary
equilibrium pressure-surfaces. The so called triangle-diagrams are as well-known
in Chemistry as in Mathematics the C' surfaces over the basic R2
simplex. But there is not any graphic software available that can plot
a surface over a non-rectangular region. In this figure we are showing
the graphic result of our own PASCAL program where one can obviously see
the binary pressure curves: the boundaries of the ternary pressure surface.
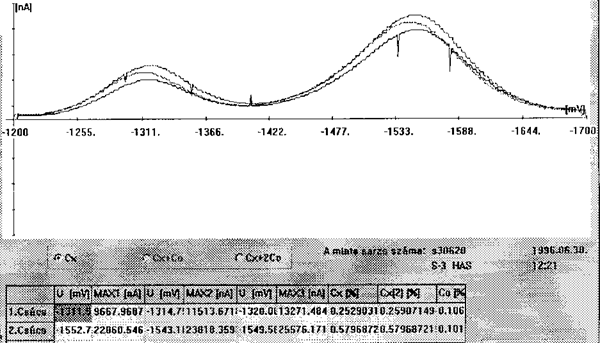
Our second example in which our own program is inevitable is an interface
program for polarograph used for data collection and evaluation. This figure
is showing in the first window the polarogram before filtering and in the
second window the measured data.
Statistics and Television Courses
Brevard Community College, along with Daytona Beach Community College
and Valencia Community College, has recently been selected by the PBS Adult
Learning Service of the United States as one of 20 model college partnerships
in a unique pilot project for Going the Distance: The Distance Learning
College Degree Project. The goal of this project is to provide
distance learning courses that lead to an A.A. degree in General Studies.
A telecourse is an integrated learning system that contains televised lessons,
related assignments, optional on-campus review oppurtunities and minimal
required on-campus sessions for orientation, discussions and examinations.
BCC has offered telecourses since 1974 and they experienced a dramatic
increase in telecourse student enrollment to 3,500 students for the academic
year 1993-94.
It is difficult to measure, that the most profound impact is felt by
the students selecting the distance learning experience to meet their unique
needs. Citing the words of several students enrolled in BCC's telecourses
during Fall 1992:
- "TV courses are great for me because I work 9-5, Mon-Fri. I
can record the class and watch it over the weekend."
- "I have enjoyed the TV viewing and it was very good for me
as a mother of 3 under 5. Without the TV courses I could not have taken
some classes."
The TV STATISTICS (STA 2014) is a 3-credit-hour-class required
in the Quality Assurance direction. It consists of four on-campus
meetings (orientation, 1. and 2. Test, Exam) , 26 half-hour-TV lessons
, ten homework exercises in two groups and advising hours (4-6 hours/week)
when the students may call the instructor or have a walk-in consultation.
In Table 4. we are showing the time-schedule of STA 2014 with
the covered chapters and assignments of the textbook by Moore and Mc. Cabe
(1993), the units of the Telecourse Study Guide by Moore (1993) and the
tests scheduled in the BCC's summer term '95 .
Table 4. TV Statistics - time schedule
| Chapter # |
Unit # |
Topics |
Homework |
Test |
| 1. |
1,2,3,4,5. |
Describing distributions |
1.23. ; 1.51. ; 1.92. |
|
| 2. |
6,7,8,9,10,11. |
Relationships, Correlation |
2.23. ; 2.65. |
|
| 3. |
12,13,14. |
Blocking and Sampling |
|
1. Test |
| 4. |
15,16. |
Random Variables |
4.12. ; 4.89. ; 4.96. |
|
| 5. |
17,18. |
Binomial distribution, Control charts |
5.50. |
|
| 6. |
19,20. |
Confidence intervals, Significance (u,t) tests |
|
|
| 7. |
21,22. |
t-test for one meanu and t test for two means |
7.44. |
|
| 8. |
23.24. |
Inference for proportions and two-way tables |
|
2. Test |
| 9. |
25.26. |
Inference for relationships |
|
Exam |
In our experiences this type of time and assigment's schedule have developed
a good learning habit in the students. Due to the large amount of homework
in the first 3-4 weeks, for the later chapters that are not accompained
by the same amount of assignments or for the last ones that aren't discussed
in every detail, the students acquired an ability to see and extract the
most important parts.
At the Chemical Faculty of TUB we teach Statistics in five different
courses, directions or levels: Mathematical Statistics - this covers the
principles of Probability and Statistics for the B.Sc students ; Biometry
- which is the same principal course for the students in the Biological
Engineering direction, Design of Experiments and Chemometry - these are
facultative classes at the M.Sc. or Ph.D. level.
Three years ago the Chemical Engineering Faculty developed a MULTIMEDIA
classroom for 300 students. This new classroom offers the possibility to
develop a videotape oriented course similar to the BCC's TV course. At
the same time we are able to make the whole videotape series available
in our library or even in the HUNGARIAN DISTANCE LEARNING PROGRAM of
the TUB and the UHFI. This last program is extremely important with respect
to our neighbour-countries where the possibility of studying in Hungarian,
broadened with a new aspect for the Hungarian minority living there.
Acknowledgement
The authors wish to express their gratitude to the CCID/USA, to S. M.
Campbell, to N. Harbour and to Prof. Dr. D. Argo (BCC/UCF), to the Hungarian
National Research Foundation OTKA (grant # T-023258) and to the Ph.D. and
voluntary research students of the TUB, N. S. Ha, K. Hermann, N.B. Thuy,
J. Heszberger and I. Berente.
References
- Berry, J.S. and Watkins, A.J.P., Learning Mathematics through DERIVE
(ISBN 0-13-037532-2) Ellis Horwood , New York, 1993
- Zill, D.G., Calculus with Analytical Geometry (ISBN 0-534-92793-9)
PWS Publ. Comp., Boston, 1992
- Moore, D.S., Telecourse Study Guide: "Against All Odds" (ISBN
0-7167-2452-9) Freemann Co., New York, 1993
- Moore, D.S., and Mc. Cabe, G.P.: Introduction to the practice of statistics
(ISBN 0-7167-2250-X) Freemann Co., New York, 1993
 As a
very interesting example we show first the quite simple problem of ternary
equilibrium pressure-surfaces. The so called triangle-diagrams are as well-known
in Chemistry as in Mathematics the C' surfaces over the basic R2
simplex. But there is not any graphic software available that can plot
a surface over a non-rectangular region. In this figure we are showing
the graphic result of our own PASCAL program where one can obviously see
the binary pressure curves: the boundaries of the ternary pressure surface.
As a
very interesting example we show first the quite simple problem of ternary
equilibrium pressure-surfaces. The so called triangle-diagrams are as well-known
in Chemistry as in Mathematics the C' surfaces over the basic R2
simplex. But there is not any graphic software available that can plot
a surface over a non-rectangular region. In this figure we are showing
the graphic result of our own PASCAL program where one can obviously see
the binary pressure curves: the boundaries of the ternary pressure surface.