
1. Melusina-ábrázolások egy alkimista
szövegben
A rendetlenség reménye
Ó, hogy nem tud kiszakadni belôlem
a lélek...
Németh László: Galilei, III. felvonás1
"A testi világot abban az idôben még nem fosztották meg teljesen a lélektôl; ezt csak Newton Principiája végezte be. Kepler számára a bolygók még egyéni lélekkel megáldott élôlények voltak." Wolfgang Pauli, a század elsô felének egyik legkritkusabban gondolkodó elméleti fizikusa írta ezt Kepler koráról.2 Keplert ez a meggyôzôdése vezette el tulajdonképen a heliocentrikus világnézethez. Az ô istenképe, pontosabban Szentháromság-képe a legtökéletesebb idom, a gömb volt. Középpontja az Atya, felszíne a Fiú és a kettô közötti tér a Szentlélek. És ahogyan középpont, felszín és térfogat egymástól elválaszthatatlanul jelenik meg, ahogyan hárman csak együtt létezhetnek, úgy alkot elválaszthatalan Egységet a Háromság. A geométer számára a hit, úgy látszik, nem misztikus megvilágosodás, hanem térbeli modell kérdése.
Az anyag képe a sík volt Kepler világában. Az anyagi sík és az isteni gömb metszete szabja meg a bolygók pályáját, a kört, középpontban a sugárzó Nappal. A körpályákhoz egy-egy gömbfelületet tartozik, a gömbök sugarait pedig a beléjük és köréjük írható tökéletes platoni testek: a kocka, tetraéder, dodekaéder, oktaéder és ikozaéder határozzák meg. Szigorú geometriai rend uralkodik ebben a világban, még a Teremtô szándékát is eleve ez határozza meg. Esetlegességet, véletlent nem ismer a világkép.
Kepler intellektusának erejét két teljesítményén szokták mérni. A bolygómozgás három törvényének felismerésén, és azon a módszeren, ahogyan a Mars látszólagos pályájából kiszámította a pálya valódi alakját. Én szívesen hozzáfûzném harmadiknak azt az önkínzó lelkiismeretességet, amellyel Tycho Brahe mérési eredményeit összehasonlította a fenti világképpel, majd úgy találva, hogy a Mars pályája nyolc ívperccel eltér a tökéletes körtôl, alapjában megváltoztatta elképzelését a teremtésben uralkodó rend természetérôl. Tudta, hogy Tycho mérései két ívperc pontosságúak.
Amin nem változtatott, az az eleve elrendelt, véletlentôl meg nem zavart rendbe vetett hite volt. A bolygók mozgása fölött szigorú, az idôk végezetéig állandó törvény az úr. A Keplerrel és Galileivel kezdôdô, Newton munkásságában kiteljesedô és a mi századunk húszas éveiig tartó tudományos korszak nagy célja: az elôrelátás. A fizika törvényeinek nemcsak az a feladata, hogy az észleleteket rendbe fogják, hanem az is, hogy a természetben majd bekövetkezô eseményeket meg is jósolják. Schrödinger írja errôl a korszakról: "Az abszolút determinizmus úgyszólván a klasszikus fizika alapvetô dogmájává lett. A legáttekinthetôbb példa, amelyet követni akartak, a klasszikus mechanika volt. Ott a tömegpontok egy meghatározott rendszerét vizsgáljuk: ismerjük minden pont tömegét, helyét és sebességét valamely kezdeti idôpontban, ismerjük a köztük ható erôket is. Ha ennyit tudunk, úgy elôre ki tudjuk számítani, hogy hogyan fognak a pontok mozogni bármelyik tetszôleges késôbbi idôpontban. Az elméletet az égitestekre való alkalmazása igazolta, ragyogóan."3
Ez persze utólagos, szinte nosztalgikus jellemzése a nagy korszaknak; az idézet 1932-bôl, a kvantummechnika megalkotása utáni idôbôl származik, akkorról tehát, amikor a fizikusok kénytelenek voltak megtanulni, hogy a szigorú determinizmus egy fizikai elméletnek nem föltétlen attribútuma. Ez a kérdés a klasszikus fizika korának mitha nem lett volna eleven gondja.
Pedig a legnagyobbak természetesen nemcsak aktuális feladatban, hanem világképben is gondolkodtak. A gondolkozás eszközeinek a dolgában sem voltak ösztönös alkotók. Fehér Márta és Vekerdi László tanulmányaira hivatkozom itt csak a nagyon sok közül.4,5 Galilei, a Discorsi kiadói elôszava szerint, "mindig szem elôtt tartotta, hogy - mint mondani szokták - a tapasztalat egyetlen nap alatt többre és jobban megtanít, mint az ezerszer ismételgetett elvek, de azt is (így szól a másik jó tanács), hogy az intuíció járjon karöltve a definíciókra épített tárgyalással". Newtont megfigyelés, dedukció és indukció, axióma és hipotézis problémája foglalkoztatta. A megfigyelhetô és a létezô, de elvileg megfigyelhetelen viszonya. Jelenségek és okok kapcsolata, tehát a kauzalitás problémája. Az erô a mozgás oka? Vagy létezik valami mélyebb ok?
Vagy úgy van, ahogyan késôbb Hume gondolta, hogy egyidejûségek léteznek csak (ezeket valóban megfigyelhetjük), oksági kapcsolatokra azonban ezekbôl nem következtethetünk? Mert Hume szerint: "A történések különállóaknak és egymástól teljesen függetleneknek látszanak. Az egyik történés követi a másikat; de soha semmilyen kapcsolatot nem tudunk megfigyelni köztük. Együtt jelentkeznek, de soha sincsenek összekapcsolva."6
A kapcsolatnak ez a hiánya azonban, úgy látszik, nem korlátozza elôrelátásunkat. Mert ezt is olvashatjuk: "De ha bizonyos fajta történések mindig, minden esetben egymáshoz kapcsolódtak, akkor az egyikbôl már tétovázás nélkül megjövendöljük a másikat." Ebbôl azonban, mondja, még nem szabad arra következtetnünk, hogy oksági összefüggés áll fenn ezek között a történések között. Amit kauzalitásnak nevezünk, az csak "elménkben érzett kapcsolat, a képzeletnek ez a szokásos átváltása az egyik dologról a megszokott kisérôjelenségre, ez tehát az az érzet vagy benyomás, amelybôl az erô vagy a szükségszerû kapcsolat eszméjét kialakítjuk".
Ami itt a mai olvasót meglepheti -- a XVIII. század ezt bizonyára természetesnek találta --, az talán nem is az oksággal szemben tanúsított szélsôséges szkepszis. Inkább a determinizmust illetô bizonyosság. Annak a tapasztalatnak a kétséget nem ismerô elfogadása, hogy bizonyos események, jelenségek mindig együttesen, szigorú egymásutánban következnek be. Hume kritikája az ebbôl a tapasztalatból következtetett (és közvetlenül meg nem tapasztalható) oksági viszony föltevésére vonatkozik. Abban a kérdésben, hogy valamely eseményre mindig egy meghatározott másik következik, abban a kérdésben se kételye, se fenntartása nincsen. A jelenségek között nem áll fenn okozati kapcsolat. Tapasztalataink szerint azonban elkerülhetetlen, hogy ne kövessék egymást szigorúan elôírt sorrendben. Nem kauzálisak az események. Az események determinisztikusak.
És ahogy a jelenségek az egyenletesen múló idôben mennek végbe, csak olyan természetes biztonsággal foglalják el helyüket Euklidész háromdimenziós terében. Hiszen a földi és égi mechanika newtoni egyesítése éppen azon az eszmén nyugszik, hogy az égitestestekek ugyanúgy van helye, kiterjedése és pályája, mint ahogy azt a Földön mozgó testekkel kapcsolatosan tapasztaljuk. A köztük ható erôk is olyanok, mint amilyeneket a Föld felszínén mérhetünk.
A véletlen, az esetlegesség a természet leírásának egy más területén uralkodott, még Galilei és Kepler kora után is. Az anyag lelkének diszciplinája, a természetnek nem-természettudományos birtokbavétele ez: az alkímia. Kutatásaik területe szerint az alkimistát és a fizikust nem kellett volna egy világnak elválasztania egymástól. Voltaképpen nem is érezhették ezt a dikhotómiát olyan élesnek: Newton koponyájában jól megfért egymással a két terület. Mai eszünk szerint sem az a baj, hogy a XVII. és XVIII. század kémiai ismeretei hiányosabbak voltak, mint a mechanikaiak, ezért az utókor fölényével mosolyoghatunk azon a naiv erôfeszítésen, hogy az emeberek aranyat akartak csinálni. Hiszen, bölcsen tudjuk, az arany kémiai elem. Amit igazából csak onnan tudunk, hogy hosszas próbálkozások ellenére sem sikerült aranyat csinálni. Tekinthetnénk tehát úgy az alkímiára, mint a tudományos kémia korai, tapasztalatgyûjtô korszakára. Tisztelheténk úgy ôs-vegyészként Hermész Triszmegisztoszt, ahogyan ôs-kozmológusként Ptolemaioszt tiszteljük. A téves fogalmai ellenére is nagy rendszeralkotót. Nem így szoktunk gondolni az alkímiára.
Tudjuk jól,7 az alkimista -- a szó eredeti, de még Newton idejében is élô értelme szerint -- természetesen nem szélhámos aranycsináló, aki vasdarabra kicementált rézbevonatot mutogat színaranyként. Hisz ô ugyan a "transzmutáció", a "tingálás" lehetôségében, azt is állítja talán, hogy ô maga ért hozzá, de nem pusztán ebbôl a célból hevíti kemencéjét, vet alá destruktív desztillációnak minden, keze ügyébe akadó anyagot. Az aranycsináló csaló képe, noha persze korábban is fel-feltûnt, hiszen a gazdagságot, a gazdagság legkézzelfoghatóbb és ugyanakkor legrejtélyesebb szimbólumát mindenkor áhították az emberek, igazából csak a XVIII. században vált uralkodóvá. Sok egyéb mellett talán azért is, mert addigra, éppen a kísérleti természettudományok kialakulásával és megerôsödött tekintélyével, a kísérleti bizonyíték igénye uralkodóvá vált. Az alkimista tanításnak legnyomatékosabb kísérleti bizonyítéka pedig kétségkívül egy szépen fénylô, "jó minôségû" (így mondták) aranyrög lett volna, amely valamely recept szerint az alkimista kápolnájában és az ô keze nyomán keletkezett. (A kápolna nem az áhítat helye -- a magyar alkimisták így hívták az izzítókemencét, bizonyára boltozatos teteje miatt. Amibôl megint csak nem következik, hogy az áhítatnak nem volt nagy szerepe az alkimista munkáiban.)
A klasszikus fizika és az alkímia között, egyéb, nagyon lényeges vonásokon túl, a nagy különbség abban áll, hogy a fizikus úgy tudja, a testek közötti kölcsönhatások a megfigyelt vagy kisérleti úton megvalósított változásokban maguktól megnyilvánulnak. Az alkimista azt hiszi, az anyagokban rejlô tulajdonságok a laboratórium eszközeivel felszínre kényszeríthetôk. Mesterségének neve "scientia separationis", az elválasztás tudománya. Hevíteni, párolni, oldani, kristályosítani, olvasztani kell az anyagokat, majd szétkényszerülnek akkor az összetevôik, amelyek elemi formájukban változatlanok és elpusztíthatatlanok. Nem a változások törvényeit keresi az érintetlen természetben. Színvallásra és engedelmességre akarja bírni az uralma alá vont természetet. Azt hiszem, legfôképpen ebben a különbségben áll az, ami miatt az alkímiát semmi módon nem tekinthetjük tudománynak. A természetet nem leírni akarják, nem megérteni, bármit is jelent egyébként ez a szó. Fölébe akarnak kerülni a természetnek, testen és anyagon kívül esô törvények és öszefüggések birtokába akarnak kerülni. (Jung ennél is többet mond: szerinte az alkimista még Istennek is fölébe akar kerülni.8)
Ez nem nagyon tudományos törekvés. És persze nem is nagyon istenes törekvés. Nem véletlenül szoktak alkimista mágiáról beszélni.
Az anyag lelkének a diszciplinája, írtuk az elôbb az alkímiáról. Nem volt pontos a szó. Ha korábban nem, hát Paracelsus óta minden alkimista, minden misztikus gondolkodó tudta, hogy a világ anyagi és a lelki princípiumai mellett ott áll harmadikként a szellemi is. Mercuriusnak nevezték el ezt a princípiumot. Egyfelôl, mert ez a bolygó áll legközelebb az arany Naphoz, és a szellem a transzmutáció eszköze, esetleg maga a Bölcsek Köve. Másfelôl, mert könnyen mozgó, kiszámíthatatlanul áramló ez a szellem, mint a higany. Ahogyan Jung írja: "ez az alkimistákat a kétségbeesésbe kergetô, tûnékeny, csalfa és gunyoros kobold".9
 |
|
1. Melusina-ábrázolások egy alkimista |
Mégis, a kiszámíthatatlan Mercurius a fôszereplôje a legtöbb alkimista mûveletnek, ô a kémiai átalakulásokban állandóan tetten érhetô véletlen ura. A kézben nem tartható és ezért nem is irányítható folyamatok jelképe, a folyékonyság szelleme. Ôbenne él a középkori tündérmesék szép hableánya, Melusina. Melusina, aki kora-középkori regébôl lett alkimista szimbólummá, idô jártával megint csak népmesei alak lett. A természetet vizsgálók elfelejtkeztek róla.
El, hiszen írtuk, a szabatos megfigyeléseken és kísérleteken alapuló fizika a legtermészetesebb módon hitt a determinizmusban. Törvényei, ha egyszer a tapasztalattal összhangzónak ismerték el ôket, szükségképpen leírták a jövôbeni eseményeket. Ebben a kiszámítható világképben a kiszámíthatatlanságnak nem maradhatott helye. Már amennyiben kiszámítható minden.
Dehát a kiszámíthatóságnak szigorú korlátai vannak, még a klasszikus fizikában is. A Newton idejét követô, matematizált természetleírás az infinitezimálszámítás eszközeivel él. A természeti törvényeket differencálegyenletek formájában adja meg; a megfigyelések, mérések eredményeit (tehát a tapasztalatokat) ezeknek az egyenleteknek a megoldásaival kell összehasonlítanunk. A differenciálegyenletek megoldásához azonban, úgymond, kezdeti feltételeket kell kirónunk. Ezeket a feltételeket az egyenletek nem tartalmazzák, tôlük független információkra vagy feltevésekre kell hagyatkoznunk.
Arról van szó, hogy bármilyen kijelentést is akarunk tenni a jövôre nézve, ahhoz tudnunk kell, hogy egyszer, egy kiszemelt pillanatban, ha úgy tetszik, "kezdetben", milyen viszonyok uralkodtak. Ha egy gyerek elgurít a hegy tetején egy hólabdát, meg lehet (elvben legalább is) mondani, lesz-e ebbôl lavina. Persze, de csak akkor, ha tudjuk, hogy hol állt a gyerek, mekkora labda volt a kezében, és merre gurította, mekkora erôvel. Ezek a lavina keletkezésének kezdeti feltételei. Ha ezeket nem tudjuk, hiába ismerjük a lavina növekedésének, mozgásának törvényeit: nem láthatjuk elôre, hogy mi fog történni a havas lejtôn.
A fizikus tudásának ez a hiányos volta természetesen épp úgy vonatkozik a bolygók pályájára, mint a hólabdát gurító gyerekre. Talán azt kellene mondanunk, hogy a nagy fizikai elméleteknek elônye és hátránya egyaránt az általános érvényükben rejlik. Elôny, mert nagyon sokfajta esemény, jelenség leírására alkalmasak. Hátrány, mert egy meghatározott folyamat részletei nem olvashatók ki belôlük minden további nélkül. Newtonnak ahhoz, hogy mint írta "A világ rendszerét" matematikai alakba öntse, két törvényre volt szüksége. Az egyik a tömegvonzásé: a tömegek közt ható erôk a két súlypontot összekötô egyenes mentén hatnak, és a távolság négyzetével fordítottan arányosak; vagyis
erô = naptömeg · bolygótömeg / (távolság)2
A másik az, amit Newton II. törvényeként ismerünk:
erô = tömeg · gyorsulás.
Ez a két kifejezés együttesen egy differenciálegyenletet eredményez. Meg is lehet ezt az egyenletet oldani, a megoldás azt mondja meg, hogy melyik pillanatban hol tartózkodik a bolygó. Matematikusul szólva, a megoldás a bolygó pályáját leíró függvény. A jó és a rossz ebben az, hogy mivel a fenti egyenletek minden elképzelhetô bolygópályára igazak, a differenciálegyenletnek nem egy megoldása van, hanem végtelen sok. Valamilyen kör, ellipszis, hiperbola vagy parabola (egyszóval: kúpszelet) mentén kering minden bolygó, minden hold meg mûhold, minden üstökös. Meg annak mentén repül minden elhajított kô is. De hogy éppen melyiken? A válogatás a kezdeti feltételek dolga.
Az a kérdés tehát, hogy a Naprendszer kialakulásakor milyen tömegû égitestek, a Naptól milyen távolságra kezdték meg a keringésüket, mekkora kezdeti sebességgel. Ezek az adatok elégségesek is, szükségesek is ahhoz, hogy megmondjuk, melyik égitest melyik pályán mozog a végtelen sok lehetséges között. Newton maga ezeket a kezdeti feltételeket a Teremtô kezében hagyta. Nem nagyon tehetett egyebet. Így ír egy levelében: "... a bolygók jelenlegi mozgása nem származhatik kizárólag valamely természetes októl, hanem értelmes Akarat mûködésének eredménye."
Nem hiszem, hogy sok értelme volna ebben az összefüggésben Newton egyébként kétségtelen vallásos hitérôl beszélni. Ez a kijelentés nem az ôszinte hit megnyilvánulása, de nem is udvarias engedmény a vallásos világnézetnek. Az idézet -- amely a bolygók pályái és forgásai között fennálló, és Newton teóriájának keretei között csak a kezdeti feltételekre visszavezethetô szabályszerûségeire utal -- pusztán annyit állít, hogy a fizikai elôrelátásnak ezen a ponton vége van. Newton egyszerûen nem tudhatta, hogy milyen viszonyok uralkodtak a Naprendszer kialakulásakor. Ezek a "kezdeti" viszonyok szabták meg, hogy melyik bolygó milyen kúpszeleten mozog -- azóta is. Pesze, egy olyan teória, amely leírja a Naprendszer kialakulását, már eredményként szolgáltathatná azokat az adatokat, amelyek a Naprendszer newtoni leírásában kezdeti feltételekként szerepelnek. Bizonnyal olyan áron, hogy helyettük ennek a másik teóriának a kezdeti feltételeit kellene valahonnan kitalálni. Évszázadokkal késôbb, egy merôben más fizikai világkép és más matematikai módszerek birtokában Wigner Jenô változatlanul azt kívánja és reméli, hogy egyre kevesebb kezdeti feltételre szorul majd a fizikus. Ez jelenti ugyanis azt, hogy egyre jobban értjük a világot.
A fizika determinisztikus szemléletmódja a társadalomtudományban is teret hódít a XVIII. századra. Ezen tulajdonképpen nem nagyon kell csodálkoznunk. A korszak, amely az embert gépnek szeretné látni, miért ne tekinthetné a társadalmat fizikai rendszernek. Az úttörô ezen a területen, úgy mondják, Condorcet volt. A róla szóló gúnyvers szerint volt ô minden, hogy a végén semmi se legyen. Robespierre meg azt mondta róla, hogy az irók nagy matematikusnak, a matematikusok nagy írónak tartották.10 Egyszóval kissé késôn jött úri dilettáns lehetett a szakemberség növekvô tekintélye idején. Mint matematikus, valószínûségszámítással foglalkozott, a mai matematikatörténész azonban nem sok eredetiséget talál ezekben a munkáiban. Persze, balszerencséjére, Laplace kortársa volt, aki a valószínûség fogalmát és a vele kapcsolatos számítások természettudományos hasznát klasszikusként fogalmazta meg.
Kissé furcsának tetszik, hogy esetlegességrôl, valószínûségrôl beszélnek mindannyian, ahogy már évtizedekkel korábban Jacob Bernoulli is, miközben a determinizmus gondolatától nem tágít egyikük sem. No igen, a jelenségeknek, minden jelenségnek biztos elôzménye, (ha nem gondolunk Hume-ra: egyértelmû oka) van. Éppen csak mi vagyunk tudatlanok. Nem ismerjük eléggé az elôzményeket, az okokat, tudásunk hiányos, ezért sejtésekre kell hagyatkoznunk ott, ahol pedig a természetben egyértelmû törvények uralkodnak.
"Világos, hogy a Természet rendszerének mostani állapota a megelôzô pillanatban fennállott állapot következménye, és ha elképzelünk egy olyan Intelligenciát, amely át tudja tekinteni az Univerzumban található valamennyi létezô közötti viszonyokat egy adott pillanatban, úgy ez az Intelligencia képes lenne arra, hogy meghatározza e létezôk helyét, mozgását és általában hatásaikat bármely korábbi vagy késôbbi pillanatban." Ezt Laplace írta, ez a sokat emlegetett Laplace-démon természetrajza: ez az a csodalény, amely ismeri a vlágon végbemenô valamennyi mozgás kezdeti feltételét, tehát elôrelátásának nincsen határa. Condorcet is hasonló véleményen volt. (Ha az idézetek keltezését alaposan megnézi az ember, talán illendôbbnek találná, ha ezt a bölcs szörnyeteget Condorcet-démonnak neveznék.) A baj csak az, hogy mi, emberek nem vagyunk Laplace-démon; tudásunk hiányos, ezért -- de csak ezért -- szorulunk valószinûségi meggondolásokra.
Az egyes természeti jelenségek elôfordulásának valószínûségét, éppen tudásunk korlátai miatt, csak alapos, sokszor ismételt mérések, megfigyelések tárhatják fel. Condorcet ezen az úton akart járni, amikor a természetvizsgálat elveit a társadalmi jelenségek tudományos, tehát matematikai leírására akarta alkalmazni.
Most egy tudománytörténeti anekdota elsô része következik. Az orosz trónörökös Párizsban járva meglátogatta a Tudományos Akadémiát is, ahol az Akadémia örökös titkára, Condorcet üdvözölte, arra használva az alkalmat, hogy a tudomány nemzetközi támogatására bíztassa a cárevicset. Vannak olyan jelenségek -- modta --, amelyek csak hosszú idôn át, sok helyen tanulmányozva fedik fel törvényszerûségeiket. Ilyenek a társadalom jelenségei és -- Condorcet példája szerint -- ilyen a meteorológia is. Csak ha a megfelelô mennyiségû adat birtokába jutunk, tárulnak fel elôttünk az addig rejtett törvényszerûségek. Hiszen "minden azt bizonyítja, hogy az egész természet szabályos törvényszerûségeknek van alávetve ... Ez a rend csak a tények megfigyelése útján ismerhetô meg, ezek tömege és rendje szükséges ahhoz, hogy az gyenge szemünk elôtt feltáruljon." Condorcet, úgy látszik, egyaránt klasszikusa volt a tudós optimizmusának és az államhatalom tudományos célokra való megszelídítésének. (Az anekdota befejezését néhány lappal alább írom majd le.)
Az a felismerés, hogy a természet determinisztikus leírása a praxisban reménytelen, az atomelmélet modern, tehát XIX. század eleji visszatérésével vált nyilvánvalóvá. Egyszerûen azért, mert atomokból bizonnyal nagyon sok van egy mégoly kis anyagmintában is, hiszen az atomok olyan aprók, hogy nem is lehet szabad szemmel látni ôket. Ennyi sok részecske mozgásának minden kezdeti feltételét ismerni, ennyi mozgásegyenletet megoldani nyilván képtelen feladat. Hogy mennyi az ennyi, azt nagyon sokáig nem tudták megmondani. Talán nem is nagyon törekedtek kezdetben az atomok megszámlálására vagy a méreteik meghatározására, hiszen a létezésüket se vették nagyon komolyan. A vegyészek ügyes hipotézisének tekintették ôket sokáig sokan, köztük olyan titáni fizikusok is, mint Faraday. Ha valami ennyire kitér a megfigyelés elôl ...
A fizikus számára az atomhipotézist az a régi törekvés tette vonzóvá, amely mechanikai törvényekre kivánta visszavezetni a világ minden jelenségét. A század közepére megsokasodtak a szabatos hôtani megfigyelések, kialakult a termikus egyensúlyok tudománya, a termodinamika.
Kiderült egyebek mellett az is, hogy a termikus folyamatok talán legszembeötlôbb tulajdonsága az, hogy határozott irányuk van; úgy értve, hogy a termikus folyamatok különbséget tesznek múlt és jövô között. Ha egy vödör hideg vízbe belemártunk egy izzó vasdarabot, a víz felmelegszik, a vas lehûl. A múltban eltért egymástól a két anyag hômérséklete, az idô múlásával ez a különbség kiegyenlítôdik. Az egyensúly beáll. Soha az ellenkezôje nem fordul elô: a vízbe mártott vas magától melegedni és ugyanakkor a víz hûlni nem fog. Röviden: a termikus folyamatok megfordíthatalanok. Ez a felismerés neveztetik a termodinamika II. fôtételének. (A mechanikai folyamatok nem ilyenek: egy rezgô rugó mozgását szemlélve semmit nem tudunk meg arról, hogy mi volt elôbb, mi késôbb. Összehúzódik a rugó, kinyúlik, újra összehúzódik ... ebbôl nem lehet megmondani, hogy hogyan kezdôdött a dolog.)
A termikus folyamatok megfordíthatatlanságának jellemzésére vezették be az entrópia fogalmát. Egy függvény ez, a termodnamikai rendszerben uralkodó hômérsékleteknek, a benne áramló hômennyiségeknek a függvénye. Clausius olyan módon definiálta, hogy az értéke nem változik, ha a rendszer egyensúlyban van, és növekszik, ahogyan a rendszer egyensúlya felé tart. Matematikai ügyeskedés egy fizikai tény körül? No nem! A fizikai jelenség megengedte, lehetôvé tette, hogy kitaláljanak hozzá egy ilyen függvényt. Az elôbb említett rugó mozgásához nem lehetne ilyesmit kitalálni. Az irreverzibilitás, ha úgy tetszik, az entrópia növekedése, a termikus folyamatok legszembeötlôbb, legjellemzôbb tulajdonsága.
Nagyon kívánatosnak látszott, hogy a termodinamika felismert törvényeit mechanikai jelenségekre vezessék vissza. Magyarul: az atomok mozgására. Hiszen a mechanika egzaktsága volt minden fizikai elmélet példaképe. Úgy gondolták, csak azt értették meg igazából, amit a mechanika elvei szerint tudtak megmagyarázni. Egyébként nem is mindenki tartotta kivánatosnak ezt az irányzatot. Volt, aki úgy gondolta, a termodinamikusok egy új, nem-mechanikai diszciplina alapjait tárták fel. Önálló törvényekre leltek, amelyeket nem is érdemes, nem is esztétikus bizonyíthatatlan mechanikai modellek segítségével értelmezgetni.
Szerencsére elég sokan voltak, akik nem így gondolták. Például Maxwell, majd Boltzmann azon a véleményen volt, hogy amit mi hônek érzékelünk, az nem más, mint az atomok, molekulák mechanikai energiája; a hômérséklet ennek az energiának valamilyen átlaga; a nyomást a részecskék ütközése idézi elô az edény falán; az irreverzibilitást kijelölô entrópia pedig ... itt álljunk meg egy pillanatra!
A statisztikus mechanika megalkotóinak -- ez a neve a termodinamikát magyarázó atomelméletnek -- a nagy gondolata abban állt, hogy felismerték: nemcsak nem lehetséges, nem is szükséges a megszámlálhatatlanul sok részecske mozgásegyenletét tárgyalni. Elegendô, ha az energiájukat határozzuk meg, de ezt se kell "darabonként" elvégezni; nem érdekel az bennünket, hogy melyik részecskének mennyi energiája van. Hiszen egyesével úgysem tudnánk megfigyelni, megmérni ôket. Elég azt tudnunk, hogy a részecskék hányad részének van valamekkora energiája. Ebbôl már ki lehet számítani az egész részecske-sokaság energiáját, meg mindazt, ami ebbôl következik. Boltzmann zseniális módszert talált ki arra, hogy kiszámíthassuk, hogyan oszlik el a rendszer teljes energiája a részecskék között; vagyis hogy mi a valószínûsége annak, hogy egy részecske valamekkora meghatározott energiával rendelkezzék. Éppen csak hogy ennek a módszernek a lényege az, hogy használnia kell egy mennyiséget, termodinamikai valószínûségnek nevezik, amelynek az értéke nem változik, ha a rendszer egyensúlyban van, és növekszik, ahogyan az egyensúlya felé tart. És -- ez éppen a baj -- a termodinamikai valószínûségnek ez a tulajdonsága nem következik, vagy csak nagyon egyszerû esetekben következik a mechanika törvényeibôl. A II. fôtételt Botzmann nem tudta visszavezetni a mechanika törvényeire.
Még ma is az a helyzet, hogy a hôtani jelenségeket meg tudjuk magyarázni mechanikai elképzelések alapján, az atomi-molekuláris, statisztikus elmélet segítségével. Kivéve a hôtan legalapvetôbb, legszembeötlôbb jelenségét: a hôtani folyamatok idôbeni megfordíthatalanságát. Azt, amit a fizikus szakszóval az entrópianövekedés tételének hív.
Némi baj van persze a szigorúan vett determinizmus dolgában is. Ha valószínûségekkel kell operálnunk, soha nem mondhatjuk meg biztosan, hogy milyen eseményre mi következik. Csak sejthetünk, gyaníthatunk, becsülhetünk. Igaz. De -- és ez nagyon megnyugtató -- becsléseink annál jobbak lesznek, minél több részecskébôl áll a számításaink tárgya. A becslés megbízhatatlansága, szakszóval: a relatív hiba fordítottan arányos a részecskék számának négyzetgyökével. Nagyon sok részecske -- nagyon jó becslés.
Maxwellnek, Boltzmann-nak, de még késôbbi tanítványaiknak sem volt fogalmuk arról, hogy milyen nagyon sok atom, molekula van egy hétköznapi méretû tárgyban, mondjuk egy csepp vízben. Ma már ismerjük az igazi számokat. Ezért egyáltalán nem csodálkozunk azon, hogy a bennünket körülvevô tárgyak nem árulják el, hogy apró részecskékbôl vannak felépítve. Viselkedésüket valóban valószínûségi törvények kormányozzák, de a hatalmas részecskeszám az elvi valószínûségeket praktikus bizonyosságokká teszi. Makroszkópos méretû testek determinisztikusan viselkednek.
És a mikroszkópos méretûek? Egy molekula? Vagy egy elektron? Itt hetven éve már, hogy tudjuk, alapvetô baj van a determinizmus körül. Heisenberg nevét meg a bizonytalansági összefüggéseket szokták emlegetni. Az energia meghatározásával kapcsolatban ez a gond annyit jelent, hogy minél gyorsabban játszódik le egy folyamat, annál pontatlanabbul lehet csak az energia megváltozását meghatároznunk. Vannak tehát esetek, amikor nagyon bizonytalanok az energetikai ismereteink. Persze, csak ha atomi méretû részecskékrôl van szó. Dehát a makroszkópos testek ilyen atomi részekbôl vannak összetéve! Ha az összetevôk energiájában bizonytalanok vagyunk, hogyan lehetnénk biztosak az egészében? Ez valóban gond. De ha megvizsgáljuk, hogy mi a gyors és mi a lassú, megnyugtató eredményre jutunk: a bizonytalansági összefüggések nem keltenek zavart, ha a vizsgált folyamatok jóval lassabban játszódnak le, mint egy jól meghatározott idôtartam. Ez szobahômérsékleten úgy a másodperc tízbilliomod része (0,1 pikoszekundum, hogy szépen mondjuk). Ez rövid idô, de nem annyira, hogy mai kísérleti eszközeink számára ne volna hozzáférhetô. Ha ilyen gyors folyamatokat vizsgálunk, bizony bajunk is támad termodinamikával és determinizmussal. Az esetek fontos többségében azonban meg se közelítjük ezt a sebességet.
Egyszóval: a sok részecske jelenléte is, az egyes részecskék mikrofizikai bizonytalansága is kétessé tehetné a makroszkópos testek magatartására vonatkozó fizikai törvények erejét; nincsen baj mégsem a determinisztikus leírásokkal, amíg a makroszkópos test elég nagy és állapotát elég lassan változtatja.
A század elsô felében Melusina, a kiszámíthatalan merkuriális tündér, mégis feltûnt újra, elôbb a szépirodalomban. Talán nem illô errôl természettudományos kérdések kapcsán beszélni. Hiszen lehet, hogy a költô vátesz, úgy olvastuk, hogy szeme szent ôrületben a földrôl villan az égbe, de nem egészen természetes, hogy tekintete ezen a röppályán a fizikai folyóiratok tartalomjegyzékét is elôre látja. Okokról és összefüggésekrôl ezért ne is beszéljünk, tekintsük a puszta tényeket. Thomas Mann Doktor Faustusának hôse, a matematikai szigorral és a determinizmus rabságában komponáló zeneszerzô, Adrian Leverkühn, összeomlása pillanatában megvallja, hogy testi szerelmet csak az Andersen mese kis hableányától kapott.11 Ez a lény volt a mûvész önmagára mért kegyetlen szabályai között, sátáni szeretetlenségében az egyetlen, váratlan és szabálytalan engedmény?
És Kafka: Josef K. a maga számára érthetelen eleve-elrendelések között sodródik a végzete felé. Azt hiszem, emberséges tanácsot, amelyet ha megfogad, talán megtörik, megváltozik az események megfellebbezhetelen sora, ilyen tanácsot csak a kis cselédlánytól, Lenitôl kap: "Tegyen vallomást" -- mondja Leni. Nem tudom, hogy a név a Melusina beceneve-e, de Leni büszkén mutatja az ujjai között nôtt úszóhártyát. Josef és nagybátyja pedig csuromvizesen hagyja el a társaságát -- Kafka szerint nagy esô volt aznap Prágában.
Aztán a század második felére Melusina visszatért a természettudományokba is. Olyan jelenségekkel kezdtek találkozni a fizikában, kémiában, hétköznapinak és jól ismertnek gondolt területeken, ahol joggal hihette azt mindenki, hogy a tudományos elôrejelzés erejében nincsen miért kételkedenie. Az elôbb írtunk arról, hogy melyek azok a feltételek, amelyeknek teljesülniük kell ahhoz, hogy egy atomokból, molekulákból álló rendszer determinisztikusan viselkedjék. Ezek a feltételek rendre mind teljesültek. És mégis!
Jól ismert, vagy legalább is annak vélt, makroszkópos rendszerek viselkedése bizonyult egyszerre csak elôreláthatalannak. Elôször éppen egy meteorológus vette észre, hogy a légkörben lejátszódó folyamatokat nem lehet megjósolni, legalábbis abban az értelemben nem, ahogy ezt a szót Newton óta használják a tudományban. Pedig az alapvetô jelenségeket, amelyek szerepet játszanak a légkör fizikájában, külön-külön nagyon jól ismerjük: a gázáramlás, hôátadás, halmazállapot-változások törvényeit igazán alaposan tanulmányozták már. És ezek a folyamatok a legszigorúbb értelemben véve determinisztikusak. Hanem a légkörben ezeknek a folyamatoknak bonyolult kombinációi lépnek fel, egymást kölcsönösen befolyásoló jelenségek mennek végbe. Úgy látszik, itt a baj.
Egy amerikai meteorológus, Edward Lorenz a légáramlásnak azt a gyakori esetét vizsgálta, amikor az alsóbb légréteg egy kiterjedt tartományban, például a nyílt tenger fölött, egyöntetûen melegebb, mint a fölötte lévô; a melegebb levegô könnyebb, ezért fölfelé áramlik, a hideg meg lefelé: légáramlás és hôátadás egyszerre, egymást befolyásolva megy végbe. Egy ilyen folyamat differenciálegyenletei meglehetôsen bonyolultak, nem is lehet ôket papíron, ceruzával megoldani. A probléma számítógépes vizsgálata aztán arra a meglepô eredményre vezette Lorenzet, hogy a megoldások néha teljesen váratlanok, a szó szoros értelmében elôre nem láthatóak voltak. Úgy értve, hogy bármilyen elhanyagolhatóan csekély értékkel változtatta meg számításaiban például a felfelé meg a lefelé áramló levegô hôméréséklete közti különbséget, a végezetül kialakuló áramlási kép és hômérsékleteloszlás határozottan és megjósolhatatlanul különbözött az elôzôtôl.
Úgy látszik, a meteorológiai eseményeket, vagy legalábbis egyiküket-másikukat, nem lehet tetszôlegesen hosszú idôre elôre látni. (Ez a Condorcet-rôl szóló anekdota második része: ennyire bízzunk a társadalomtudományok jóserejében!)
Aztán lassan kiderült, ez az érzékenység a kiindulási állapotra, és az elôrejelzés ebbôl fakadó lehetetlensége nagyon sok fizikai és nem-fizikai problémában fellép; nagyon sok jelenséggel kapcsolatosan tapasztalunk hasonlót. Azokat a folyamatokat, amelyek szigorú makroszkópos törvényeknek engedelmeskednek ugyan, mégsem lehet elôre látni, hogy milyen módon mennek majd végbe, determinisztikus káosznak nevezzük.12
Amikor ennek a cikknek az írásába kezdtem, elhatároztam, nem engedek be a szövegbe semmilyen matematikai kifejezést. Szavakkal is kell tudni érthetôen beszélni. Most mégis szeretnék egy rövid idôre felmentést adni magamnak ez alól az elhatározás alól. Azt szeretném ugyanis egy számtanpéldán megmutatni, hogy ez az elôre nem látható váratlanság nem valami járulékos, eddig eltitkolt fizikai jelenség következménye. Nem abból származik, hogy a méréseink pontalanok, nem is abból, hogy a teóriáink rosszak. Egyszerûen az a helyzet, hogy nem lehet mindig, mindent kiszámítani.
A determinisztikus káosz név mögött mintha valami fogalmi szörnyszülött: contradictio in adiecto lappangana. A káosz az alaktalan, szervezetlen anyagban uralkodó rendetlenség, maga a zûrzavar. Determinisztikusnak pedig azt a jelenséget, folyamatot tekintjük, amely minden részletében elôre látható, maga a rend. A matematika maga a rend. Nézzük meg, determinisztikus-e mindig, minden matematikai eljárás.
Nagyon sokszor használtuk már ezt a szót, ideje megadni valamilyen operatív definícióját. Esetleg ezt: figyeljünk meg egy rendszert néhány, egymást követô idôpontban. Akkor nevezzük determinisztikusnak a rendszert, ha egy korábbi megfigyelés alapján ki tudjuk elôre számítani egy késôbbi megfigyelés eredményét. Az adatokat jelöljük rendre x1-gyel, x2-vel, .... , xn-nel, xn+1-gyel; determinisztikus a rendszer viselkedése, ha x1-tôl kiindulva sorra-rendre ki tudjuk számítani x2-t, ... xn-t.
Ne gondoljunk most fizikára vagy kémiára! Tekintsünk egy ártatlannak látszó összefüggést, egy számtani játékot, amely megszabja, hogyan kell x1-bôl kiszámítani x2-t, aztán x2-bôl x3-at és így tovább, valamilyen xn+1-ig. Nézzük ezt az egyszerû szabályt:
xn+1 = Axn(1-xn)2.
Itt A valamilyen állandó szám. Elsô lépésként írjunk valamilyen találomra választott x1 számot a jobb oldalra, (annyit azért kössünk ki, hogy az 0 és 1 között legyen), és számítsuk ki a képlet alapján x2-t. Aztán ezt az eredményt írjuk be megint a képlet jobb oldalába, és így számítsuk ki x3-at. Aztán haladjunk tovább, ahogy ez az egyszerû szabály elôírja. Van-e vége ennek a játéknak?
A matematikus akkor szakítja végét, ha úgy látja, az egymás után megjelenô számok egyre kevesebbet térnek el egymástól, majd végezetül egyenlôvé válnak, elérjük az xn = xn+1 állapotot. Ekkor mondja azt, hogy az eljárás konvergens volt, és megtaláltuk azt a számot, amely felé az x-ek sorozata konvergál. Már most azt veszi az ember észre, hogy ez az eljárás néha konvergens csak. Attól függ ez, hogy A mekkora. Ha például A = 3, az x-ek sorozata egy határozott értékhez tart. Ha azonban nagyobb A értéket választunk, bonyolódik az eredmény. Például A = 4,5 esetén, akárhányszor ismételjük is meg az eljárást, az x-ek sorozata nem fog egyetlen meghatározott számhoz tartani, hanem két érték között ingadozik majd végestelen végig. Ha pedig A egy kissé nagyobb, mint 5,3 akkor ... Hát ez az, amit az ember nem várna egy számtanpéldától! Ha A meghaladja ezt az értéket, akkor az x számok sorozata elkezd elôre nem láthatóan, "kaotikusan" viselkedni. Ahogyan haladunk elôre az x-ek sorozatában, úgy találunk midig új és egyre újabb számokra. Nincsen már határérték, amely felé a sorozat tartana, nincsen ingadozás sem több érték között: az x számok mintha teljesen véletlenül bolyonganának 0 és 1 között.
Ez azért nem egészen igaz. Ha kétszer egymás után pontosan (de pontosan!) ugyanattól az x1 kezdô értéktôl indulunk el, az egymás után következô x-ek pontosan ugyanazt a sorozatot fogják befutni mindkét alkalommal. De ha csak kevéssel (nagyon kevéssel) is eltér a két kezdô érték egymástól, úgy az x sorozatok már szélsôségesen különbözni fognak egymástól. Egy dologban hasonlítanak csak egymáshoz: a sorozatokban semmiféle hétköznapi értelemben vett törvényszerûség nem lesz fölismerhetô.
Röviden, a számtanpélda tanulsága: az iteráció determinisztikus, mert azonos kiindulás azonos sorozatot ír elô, de kaotikus, mert a számok vadul összevissza ugráló sorozatát kapjuk eredményül és ez ráadásul szélsôségesen érzékeny a kiindulási pont helyzetére.
Ez valóban számtanpélda volt, a szó eredeti jelentésében. De természeti folyamatok példája. A meteorológus Lorenz és az ôt követô kutatók: experimentátorok és teoretikusok nagy felismerése abban áll, hogy észrevették, sok olyan folyamat van a természetben, amelyik ebben az értelemben determinisztikus és kaotikus. Rajzoljuk föl a számtanpéldánk grafikonját, hogyan függ xn-tôl xn+1; egy kissé aszimmetrikus hegy képe jelenik meg a papíron. És most vegyünk egy kémiai példát!
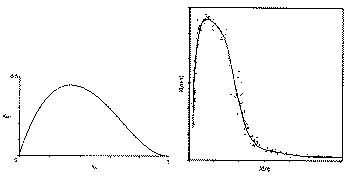 |
| 2. Bal oldalon: xn+1 mint xn
függvénye a szövegben írt képlet szerint. Jobb oldalon: egymást követô Br--ion koncentrációk egy Belouszov-Zsabotyinszkij reakcióban |
Évtizedek óta számtalan vegyész (köztük sok kiváló magyar) kutatja egy elsô rátekintésre egyszerûnek tetszô átalakulás, a Belouszov-Zsabotyinszkij reakciónak nevezett folyamat idôbeli viselkedését. Azt tehát, hogy az eltûnô, átalakuló, keletkezô vegyületek koncentrációja hogyan változik az idô múlásával. Az egyik komponens, amely ebben a folyamatban fontos szerepet játszik, a Br--ion. Most feltüntettük ezen az ábrán a Br--ion koncentrációjának nem ugyan az idôbeli változását, hanem azt, hogy az idôben egymást követô koncentrációadatok hogyan függenek egymástól. A vízszintes tengelyre rendre felmértük az 1., a 2., a 3., ..., az n-edik meghatározás eredményét, a függôlegesre pedig a 2., a 3., a 4., ..., az (n+1)-edik meghatározásét. A görbe alakja meghökkentôen hasonlít az elôbb tárgyalt számtanpélda hasonló értelmû görbéjéhez.
A kémiai tapasztalat valóban azt mutatja, hogy ez a reakció, alkalmasan választott körülmények között (vagyis ha helyesen találtuk el a kindulási koncentrációkat, a hômérsékletet és még mi egyebet, ami a reakció sebességét befolyásolhatja), a káosz tulajdonságait mutatja. A Br--ion koncentrációja összevissza változik, kétszer ugyanazt a koncentrációt soha nem mutatja a mûszer a reakció során. Ha szigorúan azonos kezdeti feltételeket tudnánk teremteni, azonos koncentrációsorozatot észlelnénk. Minthogy azonban ilyen szigorúan általában nem lehet egy kísérletet reprodukálni, az a benyomása támadhat az embernek, hogy az elegy a lombikban úgy viselkedik, ahogy kedve tartja.
Vegyész vagyok, ez az egyedüli oka annak, hogy egy kémiai példára hivatkoztam. Hozhattam volna példát a légköri jelenségek mellett az asztronómia, a szilárdtestfizika, a biológia területérôl is, hogy a közgazdaságtant vagy a társadalomtudományok egyéb területeit ne is említsem. Nagyon általános jelenségrôl van itt szó. Eleget írtunk az elôzô lapokon a kezdeti feltételek szerepérôl; azokról a mennyiségekrôl, amelyeket a differenciális alakban megfogalmazott természettörvények mellett még ismernünk kell ahhoz, hogy egy természeti folyamat sorsát leírhassuk, ha úgy teszik, a vele kapcsolatos eseményeket megjósolhassuk. Sok esetben, és ezek a hagyományos, a káosz-jelenségek felismerése elôtt vizsgált esetek, a kezdeti feltételek csak módjával befolyásolják a folyamatok sorsát. Úgy értve, hogy a kezdeti feltételek kis megváltozása csak kis mértékben hat a folyamatokra.
A kaotikus folyamatok nem ilyenek. Ezeket olyan differenciálegyenletek írják le, amelyeknek a megoldásai szélsôségesen érzékenyek a kezdeti feltételekre. A kiindulási állapot leírhatalanul kis megváltozása már nagyon nagy különbségként jelentkezik a végsô eredményben. Mintha semmi törvényt nem ismernének ezek a folyamatok. Pedig csak túlontúl jól emlékeznek születésük pillanatára, sôt korai emlékeiket még túlzó módon föl is nagyítják. Determinisztikus az ilyen folyamat abban az értelemben, hogy hajszálra egyforma kiindulás hajszálra azonos eredményre vezet. De kaotikus is ugyanakkor, mert a valóságban nem létezik kétszer egymás után hajszálra egyforma kiindulás. És kaotikus abban az értelemben is, hogy az ilyen folyamatokban a fizikailag mérhetô mennyiségek nem tartanak egy meghatározott érték felé, nem is ingadoznak néhány érték között. Mûszóval: nem stacionáriusak, mint például az egyenletesen áramló folyó vizszintje, nem periódusosak, mint például a lengô inga kitérése. Hanem -- nincsen rá jobb közkeletû kifejezés -- összevissza változnak.
Ami nem jelenti azt, hogy a determinisztikus káosz kitér minden matematikai leírás elôl.
|
|
|
3. Egy elektrokémiai folyamat különös attraktora |
Egy rajz talán megvilágíthatja, hogy mihez lehet fogni az ilyen jelenségekkel. Az ábra egy kaotikusan változó mennyiség, történetesen egy elektrokémiai cellán át folyó áram idôbeli lefutását ábrázolja, kissé szokatlan módon. A háromdimenziós koordinátarendszer egyik tengelyére a t pillantban folyó áramot mérték fel, a másik tengelyre a valamekkora idôvel késôbben folyót, a harmadikra pedig a még késôbbit. Ha ez szokványos, stacionárius (idôben állandó) folyamat lenne, a folyamat képe ezen a diagrammon egyetlen pont volna, hiszen akármennyit várnánk, mindig ugyanazt az áramot észlelnénk. Ha az áram periódusan ingadozna, egy zárt görbét, például valami ellipszisfélét kellene látnunk. Ez azonban egy kaotikus folyamat. Ezért az idôbeli változásokat leíró görbe bonyolultabb, sokszorosan megcsavart alakú, nyitott, és soha kétszer ugyanazon a ponton nem halad át. Az ilyen és ezzel rokon ábrázolásokat nevezik ebben a tudományágban különös attraktornak. A hangsúly a különös jelzôre esik; a stacionárius folyamat attraktora a pont, a periódusosé a zárt görbe.
A kaotikus folyamatok matematikai leírását talán legkönnyebben, legszemléletesebben a különös attraktorok alakjának, tulajdonságainak a segítségével végezhetjük el. Ehhez azonban a matematikának egy új, az utóbbi húsz évben kialakult diszciplináját, a fraktálok geometriáját kell igénybe venni. A fraktálokról már annyit írtak, néhány éve jelent meg például Perneczky Géza nagyszerû összefoglalója,13 hogy errôl kár lenne itt a szót szaporítani. De nézzünk csak az elôzô ábrára! A különös attraktor bejárja a tér egy meghatározott részét, egyes tartományokban sûrûn és egyre sûrûbben tekergôzik. Ha felnagyítanánk a képét, megint csak ugyanilyen alakú és sûrûségû tekervényeket találnánk. Akárhányszor ismételnénk ezt az eljárást, mindig ugyanarra az eredményre jutnánk; a képre tekintve meg se tudnánk mondani, hol tartunk a nagyítások sorában. Ha a görbe hosszát akarnánk megmérni, például úgy, hogy egy cérnaszálat fektetünk mellé, nem találnánk elég hosszú gombolyagot; végtelen hosszúnak látszanék a görbe. Szokásos görbéink nem ilyenek. Talán nem is görbe. Dehát nem is felület, vagy test ez, hiszen nem tölti ki teljesen a térnek egy darabját. Az ilyen objektumokat nevezik fraktáloknak, és azt mondják róluk, dimenziójuk nem 1, mint egy görbéé, nem is 2 vagy 3, mint egy síké vagy egy testé, hanem valamilyen törtszám. A különös attraktor ilyen törtdimenziós alakzat.
A klasszikus fizika beérte Euklidész háromdimenziós terével. A kaotikus folyamatok fizikájához új geometriára lett szükség.
És most az utolsó kérdés, a leglényegesebb. Tudnunk kellene, milyen folyamatok azok, amelyek -- legalább néha, alkalmas körülmények között -- kaotikusan viselkednek. Káosz, persze, sokféle van, nem várhatjuk, hogy valamennyi észlelt kaotikus jelenséget egyetlen szabály alá tudjunk gyüjteni. De talán ha az ellenkezô oldalról próbáljuk megközelíteni a kérdést: mikor nem lép fel semmilyen körülmények között káosz?
A klasszikus fizika elméletei általában lineárisak; az arányosság fogalma uralkodik a törvényekben. Ilyeneket szoktak mondani: a gyorsulás arányos az erôvel; az áram arányos a feszültséggel; a csôbôl kifolyó víz sebessége arányos a nyomással. Ezek a kijelentések gyakran igazak. Ilyenkor biztosan nincsen káosz. Néha azonban bonyolultabbak az összefüggések. A gyorsulás nem arányos az erôvel, mert súrlódik a test; az áram nem arányos a feszültséggel, mert felmelegszik az ellenállás; a vízfolyás sebessége nem arányos a nyomással, mert a gyors áramlás örvényeket vet. Ilyen nem-lineáris törvények esetén lehetséges a káosz. Azt mondják, ha a kiváltó ok és az okozat mértéke között legalább köbös összefüggés áll fenn, akkor van esély káosz kialakulására. (Tessék talán visszalapozni a számtanpéldánkra! Az is egy harmadfokú kifejezés.) Különösen érdekesnek látszanak ebbôl a szempontból azok az esetek, amelyek Lorenz atmoszféra-problémájához hasonlatosak. Ahol ezek a nemlineáris összefüggések nem magukban, hanem egymással keveredve-csatolva jelennek meg. Lorenz problémájában a hôátadás befolyásolja a légáramlást, a légáramlás a hôátadást. Az ilyen csatolt, nem-lineáris folyamatok könnyen válhatnak kaotikussá.
Válhatnak, de nem biztos, hogy azzá is válnak. Ezek a folyamatok csak az ôket kormányzó állandók bizonyos meghatározott tartományaiban mutatják a káosz jellegzetességeit. Éppen úgy, ahogyan a számtanpéldánkban felírt sorozat tagjai is csak A elegendôen nagy értéke mellett kezdtek veszedelmes összevisszaságban változni.
Ennyit röviden a rendetlenségrôl. És a reményrôl is. Ez nem abban áll, hogy megszüntetjük vagy elkerüljük a káoszt. Abban inkább, hogy megértjük, mikor és mitôl keletkezik. Meg abban, hogy lehetô szabatossággal megállapítjuk a tulajdonságait. Többet vagy mást a természet egyéb jelenségeivel se tehetünk.
A század harmincas éveiben ezek a jelenségek még teljességgel ismeretlenek voltak. Azt azonban, hogy a klasszikus fizika rendje felbomlott, tájékozott emberek már világosan látták. A matematikus és költô, Babits Mihály "fia és barátja", Komjáthy Aladár akkoriban ezt írta:14
| A Tér s Idô, az Isten két fia, bús tömlöctartók, szétpattanva törnek, a Semmi int zártán a földi körnek, örök s utolsó geométria. Kaosz zokog, az összedôlt Idô |
Ez a reménység.15
Megjegyzések, irodalom
1. A Németh László idézet az eredeti helyén egészen más összefüggésben jelenik meg.
2. C.G. Jung und W. Pauli: Naturerklärung und Psyche, Rascher, Zürich, 1952.
3. E. Schrödinger: Über Indeterminismus in der Physik; Ist die Naturwissenschaft milieubedingt, Barth, Leipzig, 1932.
4. Galilei: Matematikai érvelések és bizonyítások, Vekerdi László utószavával, Európa, 1986.
5. Newton: A világ rendszerérôl, Fehér Márta utószavával, Magyar Helikon, 1977.
6. D. Hume: Tanulmány az emberi értelemrôl, Szenczi Miklós utószavával, Magyar Helikon, 1973.
7. J.B. Partington: A History of Chemistry, Vol.I., McMillan, London, 1961.
8. C.G. Jung: Psychologie und Alchemie, Gesammelte Werke XII. Walter, Olten, 1972.
9. C.G. Jung: Paracelsica, Rascher, Zürich, 1942.
10. K.M. Baker: Condorcet, The University of Chicago Press, Chicago, 1975.
11. Thomas Mann a hableányt Hyphialtának nevezi; kissé meglepô ez a görögös név Leverkühn késô-középkoriasan hangzó német dikciójában. Nietzsche emlékére került ide? Talán nem is idézet valahonnan, hanem Thomas Mann saját leleménye? Etimológiája egyébként fojtogató éjszakai lidércre, succubusra utal. (Köszönöm Balassa Péter, Kocziszky Éva és Pók Lajos tanácsait ezzel a problémával kapcsolatban.)
12. A magyar nyelvû, inkább technikai jellegû öszefoglalások közül néhány cím: Szépfalusy Péter és Tél Tamás: A káosz, Akadémiai Kiadó, Budapest, 1982.; A káosz és rendezetlenség kutatása, Magyar Tudomány különszáma, 1993, 4. szám, 377-527. O.; Schiller Róbert: "Törvény és zûrzavar", Természet Világa 125, 338 (1994)
13. Perneczky Géza: Mire jó a fraktálfilozófia, a szerzô kiadása, Köln, 1992.
14. Komjáthy Aladár: Kozmogónia, in: Szavak lánca, Versek, Singer és Wolfner, é.n., h.n. (1938, Budapest) Ezzel a verssel kapcsolatban elkerülhetelen, hogy a nagy matematikus, Jacobi egy epigrammájára ne gondoljon az ember; annak az utolsó két sora így hangzik:
| Visszfény az csak az istenibôl, mit a Kozmosz elárul, mind az Olümposzi közt trónol örökre a Szám. |
15. A kézirat lezárása után olvastam csak el Földényi F. László kötetét, A Medúza pillantását, benne A káosz címû fejezetet. Vallástörténeti, lélektani és filozófiai fejtegetései nagyon messze esnek azoktól a problémáktól, amelyeket én próbáltam megvilágítani. Két dolog bizonyára nem lesz attól hasonlóvá, hogy hasonló néven emlegetik ôket. Mégsem merném azt állítani, hogy egyik-másik vonatkozásban nem írtam volna meg másként a föntieket, ha idôben találkozom ezzel a könyvvel.